Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.
class Node {
public int val;
public List<Node> neighbors;
}
Test case format:
For simplicity sake, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.
Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Example 1:
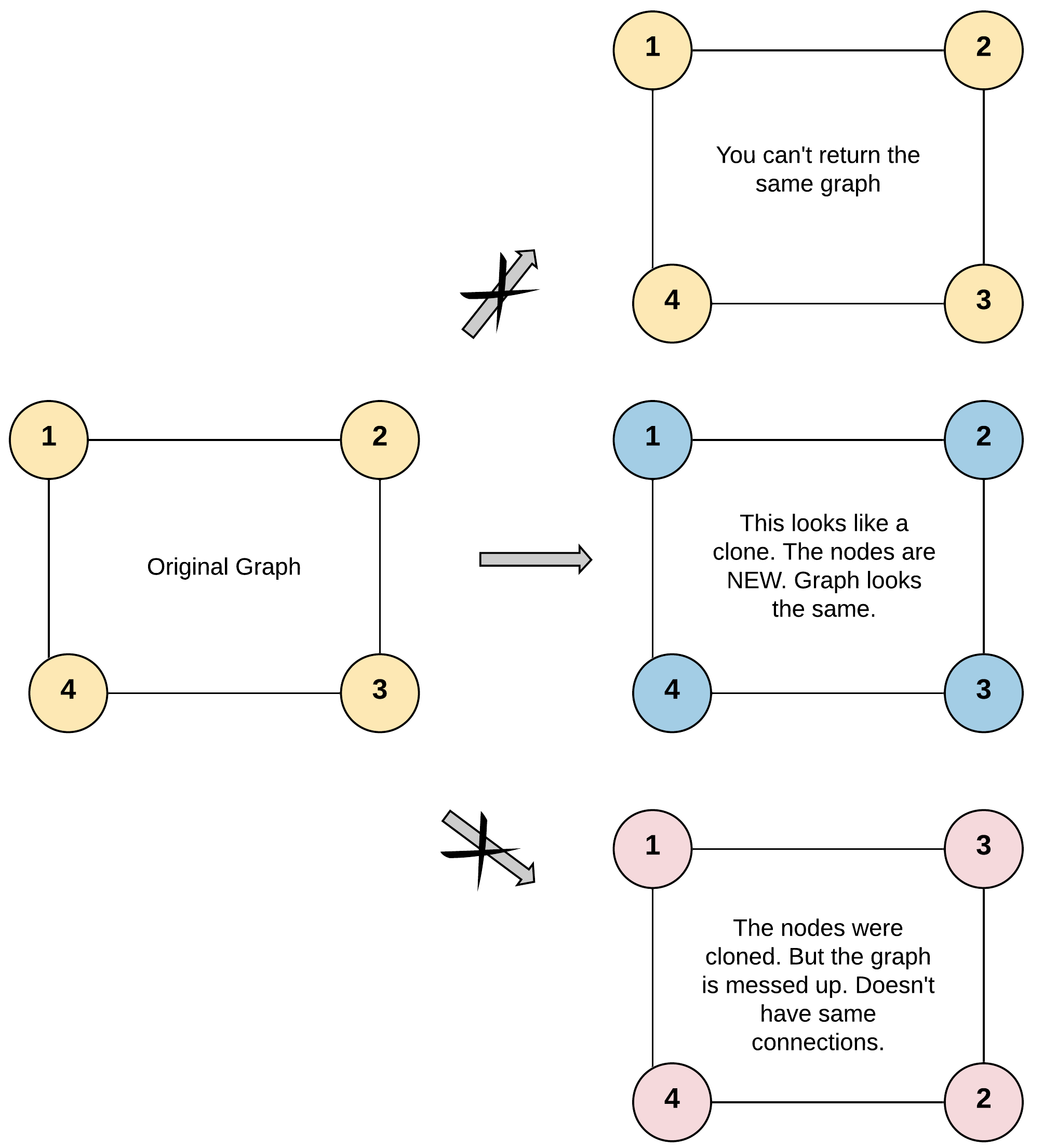
Input: adjList = [[2,4],[1,3],[2,4],[1,3]] Output: [[2,4],[1,3],[2,4],[1,3]] Explanation: There are 4 nodes in the graph. 1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4). 2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3). 3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4). 4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Example 2:
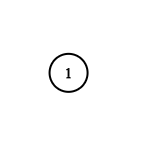
Input: adjList = [[]] Output: [[]] Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
Input: adjList = [] Output: [] Explanation: This an empty graph, it does not have any nodes.
Example 4:
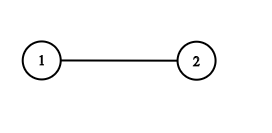
Input: adjList = [[2],[1]] Output: [[2],[1]]
Constraints:
1 <= Node.val <= 100Node.valis unique for each node.- Number of Nodes will not exceed 100.
- There is no repeated edges and no self-loops in the graph.
- The Graph is connected and all nodes can be visited starting from the given node.
给定一个无向图,要求克隆一个一样的图,也就是深拷贝。 图的问题,想到应该是DFS或者BFS,但是没太想明白,因为DFS过程中可能遇到之前已经new过的节点,不知道怎么判断比较好,查看讨论区,发现每new一个节点,把这个节点存到一个hash表中就好了,下回先查hash表,不中才new新的。 因为每个节点的label是unique的,所以hash的key可以是label,value是node*。 完整代码如下,注意第9行,new出来的节点要先加入hash,再递归DFS,否则递归DFS在hash表中找不到当前的节点,比如{0,0,0}这个样例就会出错。
class Solution {
private:
unordered_map<int, UndirectedGraphNode*> graph;
public:
UndirectedGraphNode* cloneGraph(UndirectedGraphNode* node)
{
if (node == NULL)
return NULL;
if (graph.find(node->label) != graph.end())
return graph[node->label];
UndirectedGraphNode* cur = new UndirectedGraphNode(node->label);
graph[cur->label] = cur;
for (auto& n : node->neighbors) {
cur->neighbors.push_back(cloneGraph(n));
}
return cur;
}
};本代码提交AC,用时26MS。
二刷。换了代码模板,方法是一样的,Hash+DFS:
class Solution {
public:
Node* clone(Node* node, unordered_map<int, Node*> &hash) {
int val = node->val;
if (hash.find(val) != hash.end())return hash[val];
Node *cp = new Node(node->val);
hash[val] = cp;
for (int i = 0; i < node->neighbors.size(); ++i) {
int child = node->neighbors[i]->val;
if (hash.find(child) != hash.end()) {
cp->neighbors.push_back(hash[child]);
}
else {
cp->neighbors.push_back(clone(node->neighbors[i], hash));
}
}
return cp;
}
Node* cloneGraph(Node* node) {
if (node == NULL)return NULL;
unordered_map<int, Node*> hash;
return clone(node, hash);
}
};本代码提交AC,用时12MS。