1365. How Many Numbers Are Smaller Than the Current Number
Given the array nums, for each nums[i] find out how many numbers in the array are smaller than it. That is, for each nums[i] you have to count the number of valid j's such that j != i and nums[j] < nums[i].
Return the answer in an array.
Example 1:
Input: nums = [8,1,2,2,3] Output: [4,0,1,1,3] Explanation: For nums[0]=8 there exist four smaller numbers than it (1, 2, 2 and 3). For nums[1]=1 does not exist any smaller number than it. For nums[2]=2 there exist one smaller number than it (1). For nums[3]=2 there exist one smaller number than it (1). For nums[4]=3 there exist three smaller numbers than it (1, 2 and 2).
Example 2:
Input: nums = [6,5,4,8] Output: [2,1,0,3]
Example 3:
Input: nums = [7,7,7,7] Output: [0,0,0,0]
Constraints:
2 <= nums.length <= 5000 <= nums[i] <= 100
给定一个数组，对于数组中的每个元素，计算数组中有多少个数小于这个元素。
简单题。因为数组元素的范围很小，在[0, 100]之间，所以直接用hash计算出每个元素出现的次数，然后算出前n项累加和，即可得出小于当前项的元素个数之和，最后查表即可。
完整代码如下：
class Solution {
public:
vector<int> smallerNumbersThanCurrent(vector<int>& nums) {
const int MAXN = 101;
vector<int> ans(nums.size(), 0);
vector<int> cnt(MAXN, 0);
for (int i = 0; i < nums.size(); ++i) {
++cnt[nums[i]];
}
for (int i = 1; i < MAXN; ++i) {
cnt[i] += cnt[i - 1];
}
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] > 0) {
ans[i] = cnt[nums[i] - 1];
}
}
return ans;
}
};本代码提交AC，用时12MS。
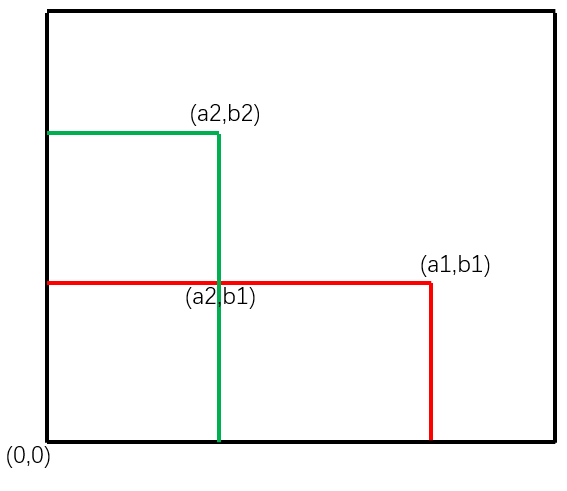所以我们只需要遍历所有操作，分别找到行和列的最小值，则他们和原点围成的子矩阵的元素值最大，且相等。
代码非常简单，如下：
[cpp]
class Solution {
public:
int maxCount(int m, int n, vector<vector<int>>& ops) {
int minRow = m, minCol = n;
for (const auto &op : ops) {
minRow = min(minRow, op[0]);
minCol = min(minCol, op[1]);
}
return minRow*minCol;
}
};
[/cpp]
本代码提交AC，用时6MS。
]]>