Find the total area covered by two rectilinear rectangles in a 2D plane.
Each rectangle is defined by its bottom left corner and top right corner as shown in the figure.
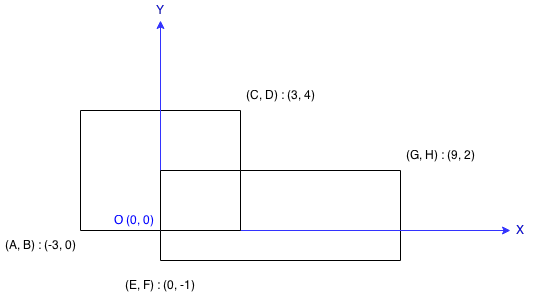
Example:
Input: A = -3, B = 0, C = 3, D = 4, E = 0, F = -1, G = 9, H = 2 Output: 45
Note:
Assume that the total area is never beyond the maximum possible value of int.
给定两个矩形,要求这两个矩形的面积和,如果有重叠区域,需要减去重叠区域的面积。因为这两个矩形的关系是rectilinear的,也就是像图中互相平行分布的,不会出现一个矩形斜着和另一个矩形相交(这样重叠区域可能是三角形或梯形)。 此题的难点是怎样判断两个矩形是否相交,肉眼很容易判断,但是怎样写一个通用程序呢。我原来的思路是先判断哪个矩形面积更小,然后判断小面积矩形是否有顶点落在大面积矩形内部,如果有则相交,否则不想交。 网上有一种比较简单的判断方法,它不判断两个矩形是否相交,而是判断两个矩形是否不相交,方法是判断一个矩形是否完全落在另一个矩形的上、下、左、右侧。因为矩形是rectilinear的,所以每侧判断只需一语句就行,比如判断图中右边那个矩形是否完全在左边矩形的右边,只需判断E>=C是否成立。 还有一种判断方法是,把两个矩形的顶点分别投影到x轴和y轴,如果投影到两个轴上的两条线段都不相交,则矩形没有重叠。 重叠之后求交集区域的面积也不难,比如上图,交集矩形x轴左端点是A,E的较大值,右端点是C,G的较小值,y轴类似。 完整代码如下:
class Solution {
public:
int computeArea(int A, int B, int C, int D, int E, int F, int G, int H)
{
int area = (C – A) * (D – B) + (G – E) * (H – F);
if (E >= C || // 右
H <= B || // 下
G <= A || // 左
F >= D) // 上
return area;
return area – (min(C, G) – max(A, E)) * (min(D, H) – max(B, F));
}
};本代码提交AC,用时22MS。
二刷。方法相同,代码如下:
typedef long long ll;
class Solution {
public:
int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
ll area1 = (C - A)*(D - B);
ll area2 = (G - E)*(H - F);
ll area3 = 0;
if (E >= C || F >= D || G <= A || H <= B) {
//没有重叠
}
else {
int ae = max(A, E), cg = min(C, G);
int bf = max(B, F), dh = min(D, H);
area3 = abs(cg - ae)*abs(dh - bf);
}
return area1 + area2 - area3;
}
};
本代码提交AC,用时12MS。