1368. Minimum Cost to Make at Least One Valid Path in a Grid
Given a m x ngrid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:
- 1 which means go to the cell to the right. (i.e go from
grid[i][j]togrid[i][j + 1]) - 2 which means go to the cell to the left. (i.e go from
grid[i][j]togrid[i][j - 1]) - 3 which means go to the lower cell. (i.e go from
grid[i][j]togrid[i + 1][j]) - 4 which means go to the upper cell. (i.e go from
grid[i][j]togrid[i - 1][j])
Notice that there could be some invalid signs on the cells of the grid which points outside the grid.
You will initially start at the upper left cell (0,0). A valid path in the grid is a path which starts from the upper left cell (0,0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path doesn’t have to be the shortest.
You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.
Return the minimum cost to make the grid have at least one valid path.
Example 1:
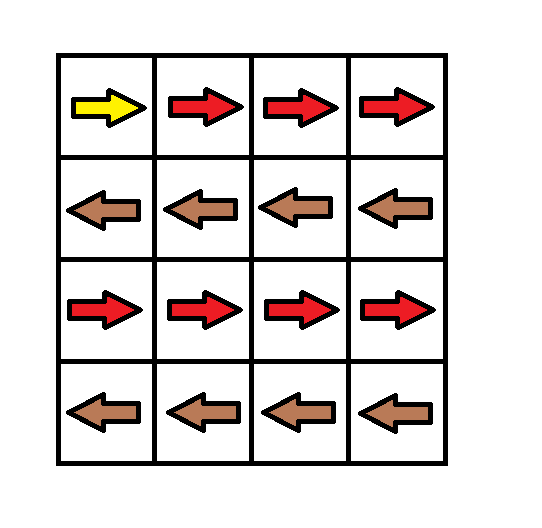
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]] Output: 3 Explanation: You will start at point (0, 0). The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3) The total cost = 3.
Example 2:
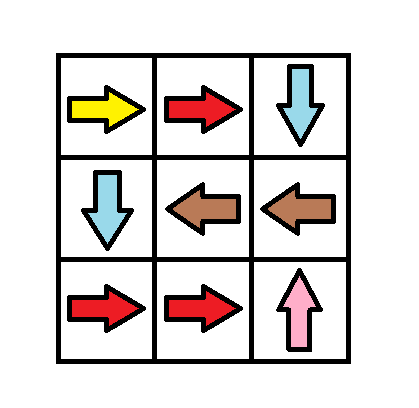
Input: grid = [[1,1,3],[3,2,2],[1,1,4]] Output: 0 Explanation: You can follow the path from (0, 0) to (2, 2).
Example 3:
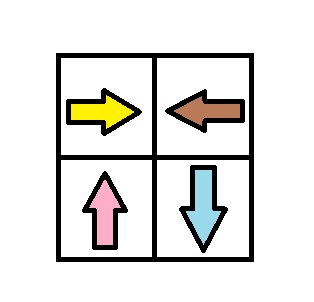
Input: grid = [[1,2],[4,3]] Output: 1
Example 4:
Input: grid = [[2,2,2],[2,2,2]] Output: 3
Example 5:
Input: grid = [[4]] Output: 0
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 100
这个题目路有点难,我想了一下午,不过想明白之后也就不难了。
给定一个网格地图,每个网格标明了从该位置可以到达的下一个位置。现在要从地图的左上角走到右下角,有可能根据图标不能到达,问最少改变几个图标可以到达。每个图标仅可改变一次,可将其改为上下左右任意一个方向。
解法1。事实上,对于网格中的每个点,它都可以走到其上下左右的4个点,只不过按图标走费用为0,不按图标走费用为1。所以可以构造一个长和宽都是m*n的图,总元素即为(m*n)*(m*n),新的图中的值就是老图中相邻两个点之间的费用。然后在新的图中执行Dijkstra算法,寻找最短路径,即为原图的最小消费。
解法1太复杂了,忘记怎么写Dijkstra了,放弃。
解法2。不转换为新的图,直接在原图中执行算法。设置一个和原图同样大小的cost二维数组,cost[i][j]表示从左上角走到该位置的最小费用。对原图从左上角开始执行BFS,如果从当前点走到下一个节点的累加费用小于下一个节点的当前费用,则更新下一个节点的费用,并且BFS走到下一个节点。最终右下角的费用就是最小费用。
完整代码如下:
const int MAXCOST = 1000000;
struct Node {
int x, y;
Node() :x(0), y(0) {};
Node(int x_, int y_) :x(x_), y(y_){};
};
class Solution {
public:
int minCost(vector<vector<int>>& grid) {
vector<vector<int>> dirs = { {0, 1}, {0, -1},{1, 0},{-1, 0} };//右左下上
int m = grid.size(), n = grid[0].size();
vector<vector<int>> cost(m, vector<int>(n, MAXCOST));
cost[0][0] = 0;
queue<Node> q;
q.push(Node());
while (!q.empty()) {
Node cur = q.front();
q.pop();
for (int i = 0; i < dirs.size(); ++i) {
int x = cur.x + dirs[i][0], y = cur.y + dirs[i][1];
if (x < 0 || x >= m || y < 0 || y >= n)continue;
if (i + 1 == grid[cur.x][cur.y] && cost[cur.x][cur.y] < cost[x][y]) {
cost[x][y] = cost[cur.x][cur.y];
q.push(Node(x, y));
}
else if (i + 1 != grid[cur.x][cur.y] && (cost[cur.x][cur.y] + 1 < cost[x][y])) {
cost[x][y] = cost[cur.x][cur.y] + 1;
q.push(Node(x, y));
}
}
}
return cost[m - 1][n - 1];
}
};本代码提交AC,用时76MS。
该解法没有设置visited数组标记走过的节点,因为没必要。一方面,以题目中的Example 2的图为例(下标从1开始),其(2,1)位置有可能从(1,1)直接下来,也有可能(1,1)先走右边下来再走左边到达(2,1),而第二条路径的费用低于第一条路径,如果设置visited数组的话,第二条路径就没法走了。另一方面,也不用担心不设置visited数组会导致程序来回来反复跑而无法终止,因为只有当走到该点的费用小于该点的当前费用时,才会将其加入队列,如果来回跑的话,费用肯定大于改点当前费用,也就不会加入队列了。所以无需设置visited数组,程序也能正常结束并得到正确结果。
解法3。参考讨论区题解,和解法2类似,但比解法2效率更高。BFS的时候,使用双端队列存储需要访问的节点,而且每次插入队列时,先插入满足原图方向标识的节点,而且是插入到队列开头,因为满足方向标识的路径费用为0,插入到队列开头之后,下次BFS时也先从队列开头取节点。对于不满足方向标识的节点,插入到队列尾部。这个策略相当于优先走费用为0的路径,只有当这些路径无法到达时,才会走费用为1的路径。
完整代码如下:
struct Node {
int x, y, cost;
Node() :x(0), y(0), cost(0) {};
Node(int x_, int y_, int cost_) :x(x_), y(y_), cost(cost_) {};
};
class Solution {
public:
int minCost(vector<vector<int>>& grid) {
vector<vector<int>> dirs = { {0, 1}, {0, -1},{1, 0},{-1, 0} };//右左下上
int m = grid.size(), n = grid[0].size();
vector<vector<int>> flag(m, vector<int>(n, 0));
deque<Node> q;
q.push_back(Node());
int ans = 0;
while (!q.empty()) {
Node cur = q.front();
q.pop_front();
flag[cur.x][cur.y] = 1;
if (cur.x == m - 1 && cur.y == n - 1) {
ans = cur.cost;
break;
}
for (int i = 0; i < dirs.size(); ++i) {
int x = cur.x + dirs[i][0], y = cur.y + dirs[i][1];
if (x < 0 || x >= m || y < 0 || y >= n)continue;
if (flag[x][y] == 1)continue;
if (i + 1 == grid[cur.x][cur.y]) {
q.push_front(Node(x, y, cur.cost));
}
else {
q.push_back(Node(x, y, cur.cost + 1));
}
}
}
return ans;
}
};本代码提交AC,用时36MS,比解法2效率更高。