Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Example:
Input: [-2,1,-3,4,-1,2,1,-5,4], Output: 6 Explanation: [4,-1,2,1] has the largest sum = 6.
Follow up:
If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.
求最大连续子数组和，这是一道非常经典的题目，从本科时候就开始做了。有两种解法。
动态规划法
用dp数组存储到当前元素的最大子数组和，如dp[i-1]表示包含第i-1个元素的最大子数组和，则dp[i]表示包含第i个元素的最大子数组和。如果dp[i-1]>0，则dp[i]=dp[i-1]+nums[i]；否则dp[i]=nums[i]。完整代码如下：
class Solution {
public:
int maxSubArray(vector<int>& nums)
{
vector<int> dp(nums.size(), 0);
dp[0] = nums[0];
int ans = nums[0];
for (int i = 1; i < nums.size(); i++) {
if (dp[i – 1] > 0)
dp[i] = dp[i – 1] + nums[i];
else
dp[i] = nums[i];
if (dp[i] > ans)
ans = dp[i];
}
return ans;
}
};本代码只用扫描一遍数组，所以时间复杂度为$O(n)$。本代码提交AC，用时12MS。
分治法
将数组一分为二，比如数组[a,b]分为[a,m-1]和[m+1,b]，递归求解[a,m-1]和[m+1,b]的最大连续子数组和lmax和rmax，但是[a,b]的最大连续子数组和还可能是跨过中点m的，所以还应该从m往前和往后求一个包含m的最大连续子数组和mmax，然后再求lmax,rmax,mmax的最大值。完整代码如下：
class Solution {
public:
int divide(vector<int>& nums, int left, int right)
{
if (left == right)
return nums[left];
if (left == right – 1)
return max(nums[left] + nums[right], max(nums[left], nums[right]));
int mid = (left + right) / 2;
int lmax = divide(nums, left, mid – 1);
int rmax = divide(nums, mid + 1, right);
int mmax = nums[mid], tmp = nums[mid];
for (int i = mid – 1; i >= left; i–) {
tmp += nums[i];
if (tmp > mmax)
mmax = tmp;
}
tmp = mmax;
for (int i = mid + 1; i <= right; i++) {
tmp += nums[i];
if (tmp > mmax)
mmax = tmp;
}
return max(mmax, max(lmax, rmax));
}
int maxSubArray(vector<int>& nums) { return divide(nums, 0, nums.size() – 1); }
};本代码可以类比平面上求最近点对的例子，需要考虑跨界的问题，时间复杂度为$O(nlgn)$。本代码提交AC，用时也是12MS。
综合来看，还是动态规划法更漂亮。
二刷。动态规划还可以再简化，即不用额外的DP数组，代码如下：
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
int max_sum = INT_MIN, cur_sum = 0;
for (int i = 0; i < n; ++i) {
if (cur_sum >= 0) {
cur_sum += nums[i];
}
else {
cur_sum = nums[i];
}
max_sum = max(max_sum, cur_sum);
}
return max_sum;
}
};本代码提交AC，用时4MS，击败98%用户。
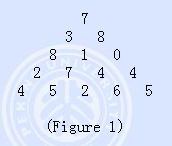Figure 1 shows a number triangle. Write a program that calculates the highest sum of numbers passed on a route that starts at the top and ends somewhere on the base. Each step can go either diagonally down to the left or diagonally down to the right.
Input
Your program is to read from standard input. The first line contains one integer N: the number of rows in the triangle. The following N lines describe the data of the triangle. The number of rows in the triangle is > 1 but <= 100. The numbers in the triangle, all integers, are between 0 and 99.
Output
Your program is to write to standard output. The highest sum is written as an integer.
Sample Input
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Sample Output
30
Source
IOI 1994