hihoCoder week 51-1-欧拉路·三
题目1 : 欧拉路·三
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi和小Ho破解了一道又一道难题，终于来到了最后一关。只要打开眼前的宝箱就可以通关这个游戏了。
宝箱被一种奇怪的机关锁住：
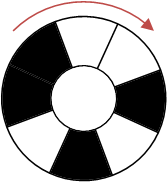这个机关是一个圆环，一共有2^N个区域，每个区域都可以改变颜色，在黑白两种颜色之间切换。
小Ho控制主角在周围探索了一下，果然又发现了一个纸片：
机关黑色的部分表示为1，白色的部分表示为0，逆时针连续N个区域表示一个二进制数。打开机关的条件是合理调整圆环黑白两种颜色的分布，使得机关能够表示0~2^N-1所有的数字。
我尝试了很多次，终究没有办法打开，只得在此写下机关破解之法。
——By 无名的冒险者
小Ho：这什么意思啊？
小Hi：我给你举个例子，假如N=3，我们通过顺时针转动，可以使得正下方的3个区域表示为：
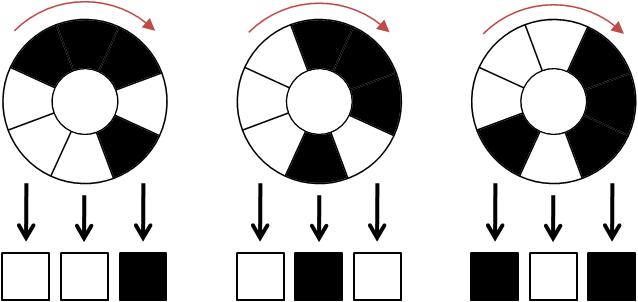因为黑色表示为1，白色表示为0。则上面三个状态分别对应了二进制(001),(010),(101)
每转动一个区域，可以得到一个新的数字。一共可以转动2^N次，也就是2^N个数字。我们要调整黑白区域的位置，使得这2^N个数字恰好是0~2^N-1
小Ho：我懂了。若N=2，则将环上的黑白色块调整为”黑黑白白”，对应了”1100″。依次是”11″,”10″,”00″,”01″四个数字，正好是0~3。那么这个”黑黑白白”就可以打开机关了咯？
小Hi：我想应该是的。
小Ho：好像不是很难的样子，我来试试！
提示：有向图欧拉回路
输入
第1行：1个正整数，N。1≤N≤15
输出
第1行：1个长度为2^N的01串，表示一种符合要求的分布方案
样例输入
3
样例输出
00010111
本题是欧拉路的判定、无向图欧拉路的求解的更进一步，有向图欧拉路的求解。 在有向图中找欧拉路的算法和无向图中相同，还是Fleury算法，只不过这一题需要自己构造有向图。构造的方法详见题目提示，我一开始根据
对于任意两个点，如果点i,点j满足点i的后n-2个数字和点j的前n-2个数字相同，则我们连接有向边(i,j)。这句话来构造的，略显麻烦。因为
而我们构造的图，由构造方法可以知道对于任意一个点，其入度一定为2，出度一定为2。所以它必定存在欧拉回路。所以对于每一个点，它有且只有两个出度，我们只需要求出这两个出度即可，不需要0~n-1一个一个点判断。用二进制表示，对于一个特定的点$$x=a_1a_2…a_n$$，假设x出边指向的点为y和z，则y,z的前n-1位和x的后n-1位是相同的，也即$$y=a_2a_3…a_{n-1}0, z=a_2a_3…a_{n-1}1$$。用公式表示就是y=(x<<1)&(111…1)，x左移一位，与上n个1，z=y+1。 把有向图构造好之后，按部就班用Fleury算法求解，再把结果倒序输出，输出的时候只要输出每个点的最后一位就行了。 完整代码如下 [cpp] #include<iostream> #include<cstdio> #include<cstring> using namespace std; const int kMaxN = 16; int edge[1 << kMaxN][2]; int path[1 << kMaxN]; int path_size = 0; int n; void MakeGraph() { memset(edge, -1, sizeof(edge)); int nn = 1 << (n – 1); for (int i = 0; i < nn; i++) { edge[i][0] = (i << 1)&(nn – 1); edge[i][1] = edge[i][0] + 1; } } void DFS(int p) { for (int i = 0; i < 2; i++) { int q = edge[p][i]; if (q != -1) { edge[p][i] = -1; DFS(q); } } path[path_size++] = p; } int main() { scanf("%d", &n); if (n == 1) { printf("01"); return 0; } else if (n == 2) { printf("1100"); return 0; } MakeGraph(); DFS(0); while (–path_size) printf("%d", path[path_size] & 1); return 0; } [/cpp] 本代码提交AC，用时8MS，内存1MB。]]>
主角继续往前走，面前出现了一座石桥，石桥的尽头有一道火焰墙，似乎无法通过。
小Hi注意到在桥头有一张小纸片，于是控制主角捡起了这张纸片，只见上面写着：
将M块骨牌首尾相连放置于石桥的凹糟中，即可关闭火焰墙。切记骨牌需要数字相同才能连接。
——By 无名的冒险者
小Hi和小Ho打开了主角的道具栏，发现主角恰好拥有M快骨牌。
小Ho：也就是说要把所有骨牌都放在凹槽中才能关闭火焰墙，数字相同是什么意思？
小Hi：你看，每一块骨牌两端各有一个数字，大概是只有当数字相同时才可以相连放置，比如：
小Ho：原来如此，那么我们先看看能不能把所有的骨牌连接起来吧。
提示：Fleury算法求欧拉路径
输入
第1行：2个正整数，N,M。分别表示骨牌上出现的最大数字和骨牌数量。1≤N≤1,000，1≤M≤5,000
第2..M+1行：每行2个整数，u,v。第i+1行表示第i块骨牌两端的数字(u,v)，1≤u,v≤N
输出
第1行：m+1个数字，表示骨牌首尾相连后的数字
比如骨牌连接的状态为(1,5)(5,3)(3,2)(2,4)(4,3)，则输出”1 5 3 2 4 3″
你可以输出任意一组合法的解。
样例输入
5 5
3 5
3 2
4 2
3 4
5 1
样例输出
1 5 3 4 2 3