1391. Check if There is a Valid Path in a Grid
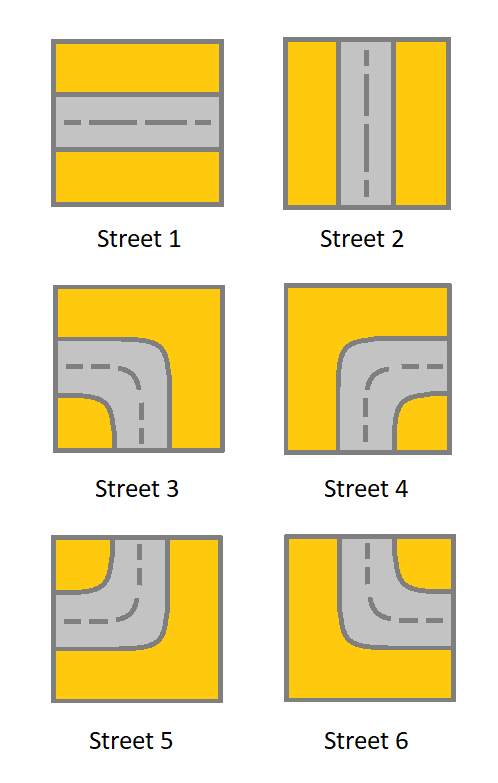
Given a m x ngrid. Each cell of the grid represents a street. The street of grid[i][j] can be:
- 1 which means a street connecting the left cell and the right cell.
- 2 which means a street connecting the upper cell and the lower cell.
- 3 which means a street connecting the left cell and the lower cell.
- 4 which means a street connecting the right cell and the lower cell.
- 5 which means a street connecting the left cell and the upper cell.
- 6 which means a street connecting the right cell and the upper cell.
You will initially start at the street of the upper-left cell (0,0). A valid path in the grid is a path which starts from the upper left cell (0,0) and ends at the bottom-right cell (m - 1, n - 1). The path should only follow the streets.
Notice that you are not allowed to change any street.
Return true if there is a valid path in the grid or false otherwise.
Example 1:
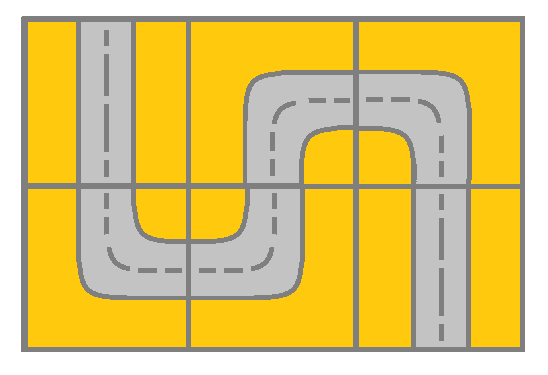
Input: grid = [[2,4,3],[6,5,2]] Output: true Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).
Example 2:
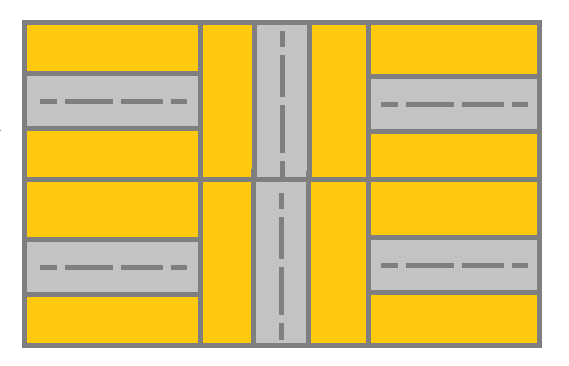
Input: grid = [[1,2,1],[1,2,1]] Output: false Explanation: As shown you the street at cell (0, 0) is not connected with any street of any other cell and you will get stuck at cell (0, 0)
Example 3:
Input: grid = [[1,1,2]] Output: false Explanation: You will get stuck at cell (0, 1) and you cannot reach cell (0, 2).
Example 4:
Input: grid = [[1,1,1,1,1,1,3]] Output: true
Example 5:
Input: grid = [[2],[2],[2],[2],[2],[2],[6]] Output: true
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 3001 <= grid[i][j] <= 6
给定一个网格,每个格子中标明了路的走向,问能否从网格的左上角走到右下角。
简单题,bfs或dfs都可以,我用的是bfs。就是在搜索的时候,各种条件比较多,写起来很费劲。
完整代码如下:
class Solution {
public:
bool hasValidPath(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> flag(m, vector<int>(n, 0));
vector<vector<int>> dirs = { {0,-1},{0,1},{-1,0},{1,0} };//左右上下
queue<pair<int, int>> q;
q.push(make_pair(0, 0));
while (!q.empty()) {
pair<int, int> p = q.front();
int u = p.first, v = p.second;
int src = grid[u][v];
if (u == m - 1 && v == n - 1)return true;
q.pop();
flag[u][v] = 1;
for (int i = 0; i < dirs.size(); ++i) {
int x = u + dirs[i][0], y = v + dirs[i][1];
if (x >= 0 && x < m&&y >= 0 && y < n && flag[x][y] == 0) {
int dest = grid[x][y];
if (grid[u][v] == 1) {
if ((i == 0 && (dest == 1 || dest == 4 || dest == 6)) ||
(i == 1 && (dest == 1 || dest == 3 || dest == 5))) {
q.push(make_pair(x, y));
}
}
else if (grid[u][v] == 2) {
if ((i == 2 && (dest == 2 || dest == 3 || dest == 4)) ||
(i == 3 && (dest == 2 || dest == 5 || dest == 6))) {
q.push(make_pair(x, y));
}
}
else if (grid[u][v] == 3) {
if ((i == 0 && (dest == 1 || dest == 4 || dest == 6)) ||
(i == 3 && (dest == 2 || dest == 5 || dest == 6))) {
q.push(make_pair(x, y));
}
}
else if (grid[u][v] == 4) {
if ((i == 1 && (dest == 1 || dest == 3 || dest == 5)) ||
(i == 3 && (dest == 2 || dest == 5 || dest == 6))) {
q.push(make_pair(x, y));
}
}
else if (grid[u][v] == 5) {
if ((i == 0 && (dest == 1 || dest == 4 || dest == 6)) ||
(i == 2 && (dest == 2 || dest == 3 || dest == 4))) {
q.push(make_pair(x, y));
}
}
else if (grid[u][v] == 6) {
if ((i == 1 && (dest == 1 || dest == 3 || dest == 5)) ||
(i == 2 && (dest == 2 || dest == 3 || dest == 4))) {
q.push(make_pair(x, y));
}
}
}
}
}
return false;
}
};
本代码提交AC,用时200MS。