LeetCode Friend Circles There are N students in a class. Some of them are friends, while some are not. Their friendship is transitive in nature. For example, if A is a direct friend of B, and B is a direct friend of C, then A is an indirect friend of C. And we defined a friend circle is a group of students who are direct or indirect friends. Given a N*N matrix M representing the friend relationship between students in the class. If M[i][j] = 1, then the ith and jth students are directfriends with each other, otherwise not. And you have to output the total number of friend circles among all the students. Example 1:
Input: [[1,1,0], [1,1,0], [0,0,1]] Output: 2 Explanation:The 0th and 1st students are direct friends, so they are in a friend circle. The 2nd student himself is in a friend circle. So return 2.Example 2:
Input: [[1,1,0], [1,1,1], [0,1,1]] Output: 1 Explanation:The 0th and 1st students are direct friends, the 1st and 2nd students are direct friends, so the 0th and 2nd students are indirect friends. All of them are in the same friend circle, so return 1.Note:
- N is in range [1,200].
- M[i][i] = 1 for all students.
- If M[i][j] = 1, then M[j][i] = 1.
给定一个矩阵,M[i][j]=1表示i和j有直接关系,如果i和j有直接关系,j和k有直接关系,则i和k有间接关系。问这个矩阵共有多少个关系网。 简单题,有两种解法。第一种解法是DFS或者BFS,每次把能搜索到的点标记为一个新的关系网,直到所有点都属于一个关系网。但是无论DFS还是BFS,复杂度都比较高。 这种题应该条件反射想到并查集,只要M[i][j]=1,则把i和j union起来,最后看一下有多少个代表就好了。这种解法非常简单,代码如下: [cpp] class Solution { private: int n; vector<int> parent; void init() { parent.resize(n); for (int i = 0; i < n; ++i) { parent[i] = i; } } int find_set(int x) { if (parent[x] != x) parent[x] = find_set(parent[x]); return parent[x]; } void union_set(int u, int v) { parent[find_set(u)] = find_set(v); } public: int findCircleNum(vector<vector<int>>& M) { n = M.size(); init(); for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { if (M[i][j] == 1) { union_set(i, j); } } } set<int> circles; for (int i = 0; i < n; ++i)circles.insert(find_set(i)); // 注意最后还要find一下找到代表 return circles.size(); } }; [/cpp] 本代码提交AC,用时19MS。]]>
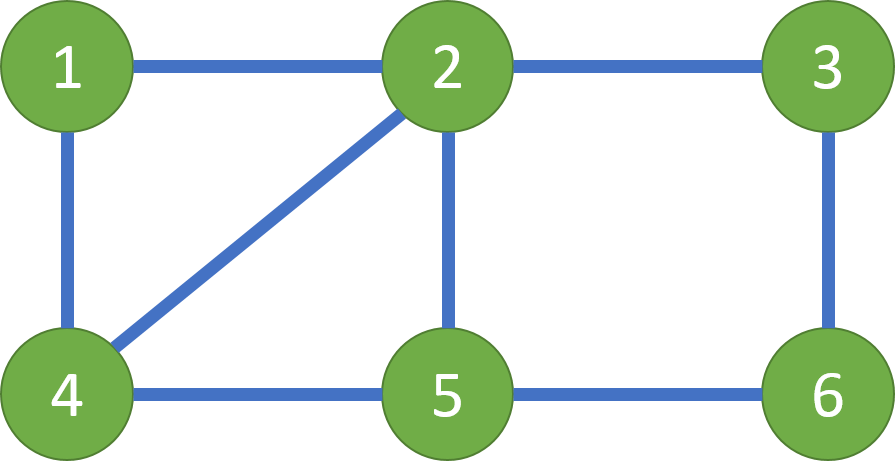 主角可以先到达4号小岛,然后按照4->1->2->4->5->6->3->2->5的顺序到达5号小岛,然后船夫到5号小岛将主角接回湖边。这样主角就将所有桥上的道具都收集齐了。
提示:欧拉路的判定
输入
第1行:2个正整数,N,M。分别表示岛屿数量和木桥数量。1≤N≤10,000,1≤M≤50,000
第2..M+1行:每行2个整数,u,v。表示有一座木桥连接着编号为u和编号为v的岛屿,两个岛之间可能有多座桥。1≤u,v≤N
输出
第1行:1个字符串,如果能收集齐所有的道具输出“Full”,否则输出”Part”。
样例输入
6 8
1 2
1 4
2 4
2 5
2 3
3 6
4 5
5 6
样例输出
Full
主角可以先到达4号小岛,然后按照4->1->2->4->5->6->3->2->5的顺序到达5号小岛,然后船夫到5号小岛将主角接回湖边。这样主角就将所有桥上的道具都收集齐了。
提示:欧拉路的判定
输入
第1行:2个正整数,N,M。分别表示岛屿数量和木桥数量。1≤N≤10,000,1≤M≤50,000
第2..M+1行:每行2个整数,u,v。表示有一座木桥连接着编号为u和编号为v的岛屿,两个岛之间可能有多座桥。1≤u,v≤N
输出
第1行:1个字符串,如果能收集齐所有的道具输出“Full”,否则输出”Part”。
样例输入
6 8
1 2
1 4
2 4
2 5
2 3
3 6
4 5
5 6
样例输出
Full
 如果op_i=0,说明这两个人是同一个集合的,即他们有共同的祖先,则首先判断这两个人在不在map中,如果不在,则以自身为祖先加入到map中,然后执行UNION操作把他们合并为一个集合。
如果op_i=1,要判断两个人是否在一个集合中,想当然的FIND他们的祖先,如果祖先相同,说明他们是一个集合的。
理清了上述关系,马上写出代码:
[cpp]
#include<iostream>
#include<string>
#include<map>
using namespace std;
map<string,string> represent;
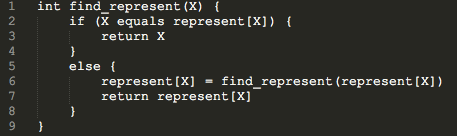
//并查集FIND操作
string find_represent(string name)
{
if(name==represent[name])
return name;
else
{
represent[name]=find_represent(represent[name]);//把经过的节点全部链接到根节点
return represent[name];
}
}
int main()
{
//freopen("input.txt","r",stdin);
int n;
int op;
string name1,name2;
cin>>n;
while(n–)
{
cin>>op>>name1>>name2;
if(op==0)
{
if(represent.find(name1)==represent.end())
represent[name1]=name1;
if(represent.find(name2)==represent.end())
represent[name2]=name2;
represent[find_represent(name1)]=find_represent(name2);//UNION操作
}
else
{
//**********也需要先判断是否在map里*********
if(represent.find(name1)==represent.end())
represent[name1]=name1;
if(represent.find(name2)==represent.end())
represent[name2]=name2;
//******************************************
if(find_represent(name1)==find_represent(name2))
cout<<"yes"<<endl;
else
cout<<"no"<<endl;
}
}
return 0;
}
[/cpp]
本代码提交AC,用时243MS,内存1MB。
需要注意的是,由于本题使用MAP实现,在执行FIND操作时有这么一句:
[cpp]
if(name==represent[name])
[/cpp]
对于STL的map,如果本来map中不存在a这个元素,执行了if(map[a]==”sth”)之后,也会自动把a加入map,最后就是map[a]=””,为空。虽然就某一次来说,这样判断的结果和下面修正的结果是一样的,但是如果下一次op_i=0需要加入a时发现map中已经有a了,就直接执行UNION操作了,但是这个时候a的祖先却是空””,而本来a的祖先应该是它自己a的。所以这就会对后面的结果产生影响。所以当我们op_i=1时,如果某个人不在map中,我们也要把它加入map并使其祖先为自身。
关于这道题,
如果op_i=0,说明这两个人是同一个集合的,即他们有共同的祖先,则首先判断这两个人在不在map中,如果不在,则以自身为祖先加入到map中,然后执行UNION操作把他们合并为一个集合。
如果op_i=1,要判断两个人是否在一个集合中,想当然的FIND他们的祖先,如果祖先相同,说明他们是一个集合的。
理清了上述关系,马上写出代码:
[cpp]
#include<iostream>
#include<string>
#include<map>
using namespace std;
map<string,string> represent;
//并查集FIND操作
string find_represent(string name)
{
if(name==represent[name])
return name;
else
{
represent[name]=find_represent(represent[name]);//把经过的节点全部链接到根节点
return represent[name];
}
}
int main()
{
//freopen("input.txt","r",stdin);
int n;
int op;
string name1,name2;
cin>>n;
while(n–)
{
cin>>op>>name1>>name2;
if(op==0)
{
if(represent.find(name1)==represent.end())
represent[name1]=name1;
if(represent.find(name2)==represent.end())
represent[name2]=name2;
represent[find_represent(name1)]=find_represent(name2);//UNION操作
}
else
{
//**********也需要先判断是否在map里*********
if(represent.find(name1)==represent.end())
represent[name1]=name1;
if(represent.find(name2)==represent.end())
represent[name2]=name2;
//******************************************
if(find_represent(name1)==find_represent(name2))
cout<<"yes"<<endl;
else
cout<<"no"<<endl;
}
}
return 0;
}
[/cpp]
本代码提交AC,用时243MS,内存1MB。
需要注意的是,由于本题使用MAP实现,在执行FIND操作时有这么一句:
[cpp]
if(name==represent[name])
[/cpp]
对于STL的map,如果本来map中不存在a这个元素,执行了if(map[a]==”sth”)之后,也会自动把a加入map,最后就是map[a]=””,为空。虽然就某一次来说,这样判断的结果和下面修正的结果是一样的,但是如果下一次op_i=0需要加入a时发现map中已经有a了,就直接执行UNION操作了,但是这个时候a的祖先却是空””,而本来a的祖先应该是它自己a的。所以这就会对后面的结果产生影响。所以当我们op_i=1时,如果某个人不在map中,我们也要把它加入map并使其祖先为自身。
关于这道题,