hihoCoder 1128-二分·二分查找 #1128 : 二分·二分查找 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 Nettle最近在玩《艦これ》，因此Nettle收集了很多很多的船(这里我们假设Nettle氪了很多金，开了无数个船位)。去除掉重复的船之后，还剩下N(1≤N≤1,000,000)种不同的船。每一艘船有一个稀有值，任意两艘船的稀有值都不相同，稀有值越小的船越稀有，价值也就越高。 Nettle现在通过大建又造出了一艘船，他想知道这艘船是不是重复的。如果是重复的，那么这艘船在Nettle所有的船里面稀有值排多少位。 问题一 Nettle已经先把自己所有船按照稀有值从小到大排列好了(a[1..N])，我们要做的是看看新得到的船(假设稀有值为K)是否在这个序列中，且有对应的a[i]=K时，i为多少？ 提示一：有序数组的二分查找 问题二 因为Nettle的船太多了，他不愿意去给所有船按照稀有值排序，而是直接告诉了我们每一艘船的稀有值。在这种情况下我们该如何解决这个问题呢？ 提示二：非有序数组的二分查找 输入 第1行：2个整数N,K。N表示数组长度，K表示需要查找的数； 第2行：N个整数，表示a[1..N]，保证不会出现重复的数，1≤a[i]≤2,000,000,000。 输出 第1行：一个整数t，表示K在数组中是第t小的数，若K不在数组中，输出-1。 样例输入 10 5180 2970 663 5480 4192 4949 1 1387 4428 5180 2761 样例输出 9
给出一串数字，问某个数字K在该序列中是第几小的。 最简单的解法，遍历一遍数组，找出比K小的数的个数n，则K是第n+1小的数。完整代码如下： [cpp] #include<iostream> #include<cstdio> #include<vector> using namespace std; vector<int> a; int n, k; int main() { scanf("%d %d", &n, &k); a.resize(n); bool is_exist = false; int ans = 0; for (int i = 0; i < n; i++) { scanf("%d", &a[i]); if (a[i] == k) is_exist = true; if (a[i] < k) ans++; } if (!is_exist) printf("-1\n"); else printf("%d\n", ans + 1); return 0; } [/cpp] 本代码提交AC，用时58MS，内存3MB。 但是题意显然不是用这种方法，为了配合下一题的求第k小数，提示使用快排的中间步骤，依次将序列划分成比某个数大和比某个数小的两部分，再在其中某个子序列中递归求解。完整代码如下： [cpp] #include<iostream> #include<cstdio> #include<vector> using namespace std; vector<int> a; int n, k; int GetOrder(int p, int q) { int m = a[p]; int i = p, j = q; while (i < j) { while (i < j&&a[j] > m) j–; a[i] = a[j]; while (i < j&&a[i] < m) i++; a[j] = a[i]; } if (k == m) return i; else if (k < m) return GetOrder(p, i – 1); else return GetOrder(i + 1, q); } int main() { //freopen("input.txt", "r", stdin); scanf("%d %d", &n, &k); a.resize(n); bool is_exist = false; for (int i = 0; i < n; i++) { scanf("%d", &a[i]); if (a[i] == k) is_exist = true; } if (!is_exist) printf("-1\n"); else printf("%d\n", GetOrder(0, n – 1) + 1); return 0; } [/cpp] 本代码提交AC，用时57MS，内存3MB。]]>
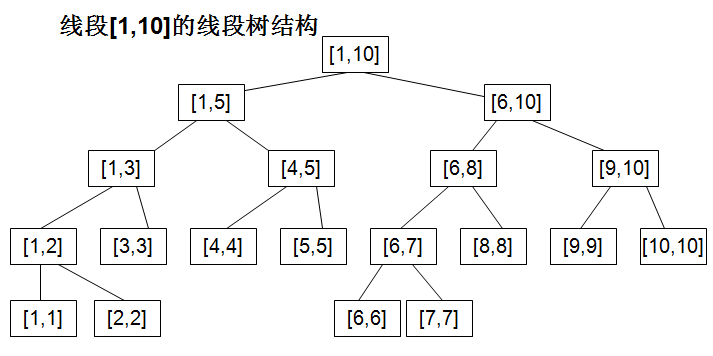从图中可以看到构造线段树的过程就是一个二分的过程，不断将区间分成两半，直到只有一个元素。图中的线段树每一个节点是一个区间[l,r]，本题我稍微改造了一下，改成了数组int seg_tree[left][length]，比如seg_tree[i][j]表示从下标i开始，长度为j的这样一个区间上的最小值，这样就可以利用线段树来解决RMQ问题了。比如改造后的线段树就成了下面的样子：
因为树形这种特殊的结构，我们可以用一个DFS来对树实现二分构造，当DFS到某个节点长度为1时，其最小值就是w[i]本身，在回溯到父节点时，父节那个区间的最小值又是所有子节点最小值中的最小值。因为树的总节点数大约为2*n，所以复杂度O(n)。
当需要查询区间[l,r]的最小值时，只需对数组seg_tree二分搜索。具体来说，假设我们搜索到了节点[s_l,s_len]，如果r<(s_l+s_len/2)，说明区间[l,r]全在[s_l,s_len]的左边，我们递归在[s_l,s_len/2]区间找；如果l>=(s_l+s_len/2)，说明区间[l,r]全在[s_l,s_len]的右边，我们递归在[s_l+s_len/2,s_len-s_len/2]区间找；如果以上两者都不是，说明[l,r]跨界了，而且中点下标一定是s_l+s_len/2，所以我们分别在二两半区间找，然后求这两者的最小值。复杂度O(lgn)。
当需要更新某个下标为pos的值为value时，也是DFS查找线段树，直到找到叶子seg_tree[pos][1]，更新它的值，以及所有我们在查找过程经过的父节点的值。复杂度O(lgn)。
所以线段是的性质使得无论是构造、查询、更新操作，复杂度都只要O(lgn)，这就是题目中所说的把总的复杂度平均分配到不同操作：平衡乃和谐之理。
完整代码如下：
[cpp]
#include<iostream>
using namespace std;
const int MAX_N=1e4+2;
int w[MAX_N];//每个商品重量
int n,m;
int seg_tree[MAX_N][MAX_N];//seg_tree[i][j]：起点为i，长度为j的区间的最小值
inline int get_min(int a,int b)
{
return a<b?a:b;
}
//深度优先遍历以构造线段树
void dfs(int left,int length)
{
if(length==1)
{
seg_tree[left][1]=w[left];
return;
}
dfs(left,length/2);
dfs(left+length/2,length-length/2);
seg_tree[left][length]=get_min(seg_tree[left][length/2],seg_tree[left+length/2][length-length/2]);//取最小值
}
//在区间[s_left,s_len]搜索区间[left,length]的最小值
int search_min(int s_left,int s_len,int left,int length)
{
if((s_left==left)&&(s_len==length))
return seg_tree[s_left][s_len];
if((left+length-1)<(s_left+s_len/2))//全在左半部分
{
return search_min(s_left,s_len/2,left,length);
}
else if(left>=(s_left+s_len/2))//全在右半部分
{
return search_min(s_left+s_len/2,s_len-s_len/2,left,length);
}
else//左右分开搜索
{
int left_len=s_left+s_len/2-left;
int right_len=length-left_len;
int min_left=search_min(s_left,s_len/2,left,left_len);
int min_right=search_min(s_left+s_len/2,s_len-s_len/2,s_left+s_len/2,right_len);
return get_min(min_left,min_right);
}
}
//从区间[s_left,s_len]开始更新下标pos的值为value
void update(int s_left,int s_len,int pos,int value)
{
if((s_left==pos)&&(s_len==1))
{
seg_tree[s_left][1]=value;
return ;
}
int mid=s_left+s_len/2;
if(pos<mid)
update(s_left,s_len/2,pos,value);
else
update(mid,s_len-s_len/2,pos,value);
seg_tree[s_left][s_len]=get_min(seg_tree[s_left][s_len/2],seg_tree[mid][s_len-s_len/2]);//更新父节点
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
for(int i=1;i<=n;i++)
cin>>w[i];
dfs(1,n);
cin>>m;
int p,l,r;
for(int i=0;i<m;i++)
{
cin>>p>>l>>r;
if(p==0)//查询
{
cout<<search_min(1,n,l,r-l+1)<<endl;
}
else//修改
{
update(1,n,l,r);
}
}
return 0;
}
[/cpp]
本代码提交AC，用时151MS，内存42MB。
]]>
Input
The first line of input will be a positive integer indicating how many data sets will be included (N). Each of the next N lines will contain the X and Y Cartesian coordinates of the land Fred is considering. These will be floating point numbers measured in miles. The Y coordinate will be non-negative. (0,0) will not be given.
Output
For each data set, a single line of output should appear. This line should take the form of: “Property N: This property will begin eroding in year Z.” Where N is the data set (counting from 1), and Z is the first year (start from 1) this property will be within the semicircle AT THE END OF YEAR Z. Z must be an integer. After the last data set, this should print out “END OF OUTPUT.”
Sample Input
2
1.0 1.0
25.0 0.0
Sample Output
Property 1: This property will begin eroding in year 1.
Property 2: This property will begin eroding in year 20.
END OF OUTPUT.
Hint
1.No property will appear exactly on the semicircle boundary: it will either be inside or outside.
2.This problem will be judged automatically. Your answer must match exactly, including the capitalization, punctuation, and white-space. This includes the periods at the ends of the lines.
3.All locations are given in miles.
Source
Mid-Atlantic 2001