297. Serialize and Deserialize Binary Tree
Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
Example:
You may serialize the following tree:
1
/ \
2 3
/ \
4 5
as "[1,2,3,null,null,4,5]"
Clarification: The above format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
Note: Do not use class member/global/static variables to store states. Your serialize and deserialize algorithms should be stateless.

序列化一棵二叉树。要求把一棵二叉树转换为一个字符串,并且能根据这个字符串反序列化回原来的二叉树。
首先我们使用LeetCode Binary Tree Level Order Traversal层次遍历的方法得到二叉树的层次遍历序列,然后把数字转换为字符串并用逗号拼接起所有字符串,遇到空节点,则用空字符串表示。比如下面这棵树,序列化成字符串为:1,2,3,,,4,,,5。本来5后面还有空串的,即3的右孩子及其孩子,但是为了节省空间,后面的空串和逗号都省略了。
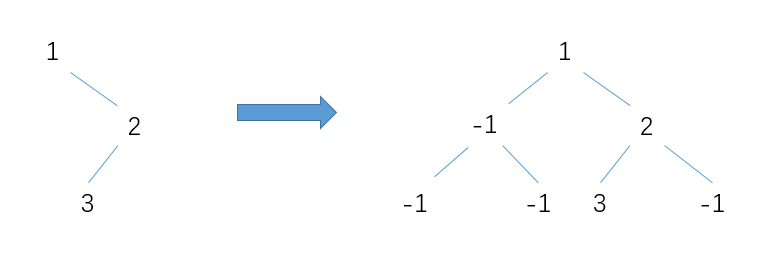
反序列化有点技巧。正常如果是一棵完全二叉树,如果下标从0开始,则节点i的左右孩子的下标分别为2*i+1和2*i+2,所以我们可以用递归的方法快速反序列化出来,就像我在LeetCode Minimum Depth of Binary Tree给出的根据数组构建树结构的genTree函数一样。对应到上图,完全二叉树的数组表示应该是{1,2,3,-1,-1,4,-1,-1,-1,-1,-1,-1,5,-1,-1},只有把这个数组传入genTree函数才能生成像上图的二叉树。
因为经过层次遍历之后的数组是{1,2,3,-1,-1,4,-1,-1,5},也就是说2后面只保留了其直接的两个空节点,并没有保留其4个空的孙子节点。导致4号节点(下标为5)在找孩子节点时,使用2*i+1=11和2*i+2=12找左右孩子的下标时,数组越界,导致漏掉了右孩子5。
后来参考了LeetCode官方的二叉树反序列化作者的介绍,恍然大悟。因为数组是层次遍历的结果,所以兄弟节点的孩子节点是按先后顺序存储在数组中的,我们可以分别维护一个父亲节点par和孩子节点child,一开始par=0,child=1,表示数组的0号节点为父亲节点,1号节点为左孩子节点,然后我们把child接到par的左孩子,把child+1接到par的右孩子,par++,child+=2,当遇到child为空,也要把空节点接到par上面。当遇到par为空时,直接跳过就好,但是child不移动。这样就能避免父亲为空,孩子节点的下标对不上的问题。比如上例中,par指向数值3时,左child指向数值4,右child指向-1;当par指向后面的两个-1时,child不动;当par指向4时,左child指向下一个-1,右child指向5正确。
完整代码如下:
class Codec {
public:
string bfs(TreeNode* root)
{
if (root == NULL)
return "";
string tree = "";
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* t = q.front();
q.pop();
if (t == NULL) {
tree += ",";
continue;
}
tree += to_string(t->val) + ",";
q.push(t->left);
q.push(t->right);
}
return tree;
}
// Encodes a tree to a single string.
string serialize(TreeNode* root)
{
string tree = bfs(root);
if (tree == "")
return "";
int end = tree.size() – 1;
while (tree[end] == ‘,’)
–end;
return tree.substr(0, end + 1);
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data)
{
if (data == "")
return NULL;
vector<TreeNode*> tree;
for (int start = 0, end = 0; end <= data.size(); ++end) {
if (data[end] == ‘,’ || end == data.size()) {
string tmp = data.substr(start, end – start);
if (tmp == "")
tree.push_back(NULL);
else
tree.push_back(new TreeNode(atoi(tmp.c_str())));
start = end + 1;
}
}
int par = 0, child = 1;
while (child < tree.size()) {
if (tree[par]) {
if (child < tree.size())
tree[par]->left = tree[child++];
if (child < tree.size())
tree[par]->right = tree[child++];
}
++par;
}
return tree[0];
}
};本代码提交AC,用时39MS。
二刷。逻辑性更好的代码:
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
vector<string> nodes;
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int n = q.size();
while (n--) {
TreeNode* cur = q.front();
q.pop();
if (cur == NULL)nodes.push_back("null");
else {
nodes.push_back(to_string(cur->val));
q.push(cur->left);
q.push(cur->right);
}
}
}
string ans = "";
int n = nodes.size();
for (int i = 0; i < n - 1; ++i) {
ans += nodes[i] + ",";
}
return ans + nodes[n - 1];
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
vector<string> nodes;
int n = data.size();
int i = 0, j = 0;
while (i < n) {
j = i + 1;
while (j < n&&data[j] != ',')++j;
string cur = data.substr(i, j - i);
nodes.push_back(cur);
i = j + 1;
}
vector<TreeNode*> tnodes;
for (int i = 0; i < nodes.size(); ++i) {
if (nodes[i] == "null")tnodes.push_back(NULL);
else tnodes.push_back(new TreeNode(atoi(nodes[i].c_str())));
}
int par = 0, child = 1;
while (child < tnodes.size()) {
if (tnodes[par] == NULL) {
++par;
}
else {
tnodes[par]->left = tnodes[child++];
tnodes[par++]->right = tnodes[child++];
}
}
return tnodes[0];
}
};本代码提交AC,用时72MS。
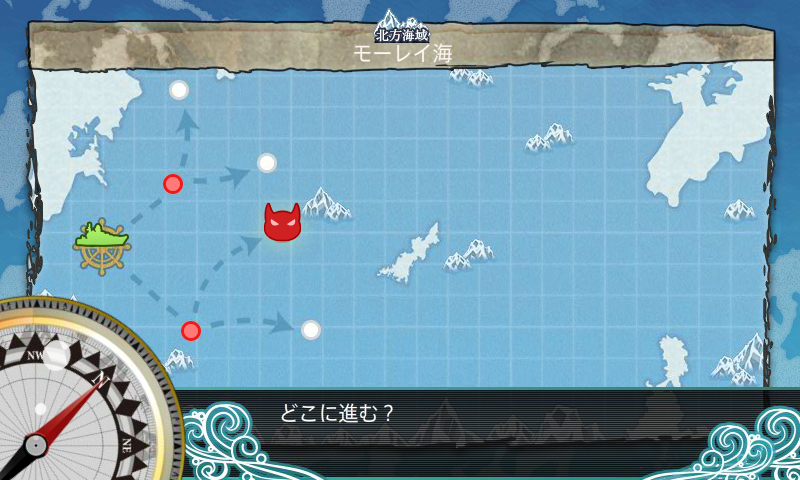 其中红色的点表示有敌人驻扎,猫头像的的点表示该地图敌军主力舰队(boss)的驻扎点,虚线表示各个战略点之间的航线(无向边)。
在游戏中要从一个战略点到相邻战略点需要满足一定的条件,即需要舰队的索敌值大于等于这两点之间航线的索敌值需求。
由于提高索敌值需要将攻击机、轰炸机换成侦察机,舰队索敌值越高,也就意味着舰队的战力越低。
另外在每一个战略点会发生一次战斗,需要消耗1/K的燃料和子弹。必须在燃料和子弹未用完的情况下进入boss点才能与boss进行战斗,所以舰队最多只能走过K条航路。
现在Nettle想要以最高的战力来进攻boss点,所以他希望能够找出一条从起始点(编号为1的点)到boss点的航路,使得舰队需要达到的索敌值最低,并且有剩余的燃料和子弹。
特别说明:两个战略点之间可能不止一条航线,两个相邻战略点之间可能不止一条航线。保证至少存在一条路径能在燃料子弹用完前到达boss点。
提示:你在找什么?
输入
第1行:4个整数N,M,K,T。N表示战略点数量,M表示航线数量,K表示最多能经过的航路,T表示boss点编号, 1≤N,K≤10,000, N≤M≤100,000
第2..M+1行:3个整数u,v,w,表示战略点u,v之间存在航路,w表示该航路需求的索敌值,1≤w≤1,000,000。
输出
第1行:一个整数,表示舰队需要的最小索敌值。
样例输入
5 6 2 5
1 2 3
1 3 2
1 4 4
2 5 2
3 5 5
4 5 3
样例输出
3
其中红色的点表示有敌人驻扎,猫头像的的点表示该地图敌军主力舰队(boss)的驻扎点,虚线表示各个战略点之间的航线(无向边)。
在游戏中要从一个战略点到相邻战略点需要满足一定的条件,即需要舰队的索敌值大于等于这两点之间航线的索敌值需求。
由于提高索敌值需要将攻击机、轰炸机换成侦察机,舰队索敌值越高,也就意味着舰队的战力越低。
另外在每一个战略点会发生一次战斗,需要消耗1/K的燃料和子弹。必须在燃料和子弹未用完的情况下进入boss点才能与boss进行战斗,所以舰队最多只能走过K条航路。
现在Nettle想要以最高的战力来进攻boss点,所以他希望能够找出一条从起始点(编号为1的点)到boss点的航路,使得舰队需要达到的索敌值最低,并且有剩余的燃料和子弹。
特别说明:两个战略点之间可能不止一条航线,两个相邻战略点之间可能不止一条航线。保证至少存在一条路径能在燃料子弹用完前到达boss点。
提示:你在找什么?
输入
第1行:4个整数N,M,K,T。N表示战略点数量,M表示航线数量,K表示最多能经过的航路,T表示boss点编号, 1≤N,K≤10,000, N≤M≤100,000
第2..M+1行:3个整数u,v,w,表示战略点u,v之间存在航路,w表示该航路需求的索敌值,1≤w≤1,000,000。
输出
第1行:一个整数,表示舰队需要的最小索敌值。
样例输入
5 6 2 5
1 2 3
1 3 2
1 4 4
2 5 2
3 5 5
4 5 3
样例输出
3
 输入
The first line contains an integer T, the number of test cases. T test cases follows.
For each test case, the first line contains contains two numbers N and M, indicating the number of modules and number of signals that Professor Q generates initially.
The second line contains M integers, indicating the signals that Professor Q generates initially.
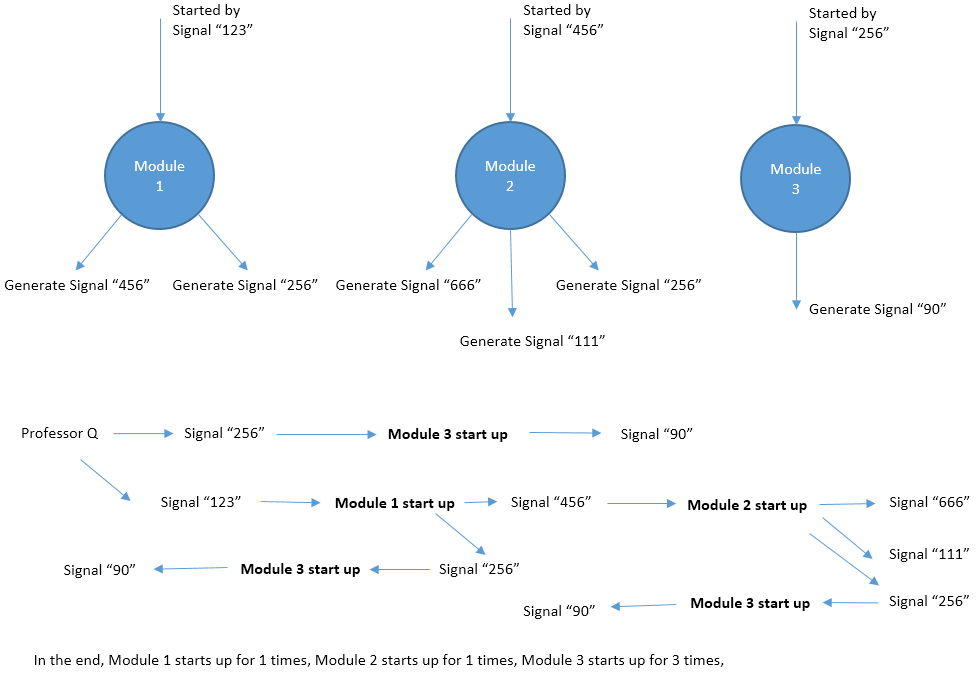
Line 3~N + 2, each line describes an module, following the format S, K, E1, E2, … , EK. S represents the signal that start up this module. K represents the total amount of signals that are generated during the lifecircle of this module. And E1 … EK are these signals.
For 20% data, all N, M <= 10
For 40% data, all N, M <= 103
For 100% data, all 1 <= T <= 5, N, M <= 105, 0 <= K <= 3, 0 <= S, E <= 105.
Hint: HUGE input in this problem. Fast IO such as scanf and BufferedReader are recommended.
输出
For each test case, output a line with N numbers Ans1, Ans2, … , AnsN. Ansi is the number of times that the i-th module is started. In case the answers may be too large, output the answers modulo 142857 (the remainder of division by 142857).
样例输入
3
3 2
123 256
123 2 456 256
456 3 666 111 256
256 1 90
3 1
100
100 2 200 200
200 1 300
200 0
5 1
1
1 2 2 3
2 2 3 4
3 2 4 5
4 2 5 6
5 2 6 7
样例输出
1 1 3
1 2 2
1 1 2 3 5
输入
The first line contains an integer T, the number of test cases. T test cases follows.
For each test case, the first line contains contains two numbers N and M, indicating the number of modules and number of signals that Professor Q generates initially.
The second line contains M integers, indicating the signals that Professor Q generates initially.
Line 3~N + 2, each line describes an module, following the format S, K, E1, E2, … , EK. S represents the signal that start up this module. K represents the total amount of signals that are generated during the lifecircle of this module. And E1 … EK are these signals.
For 20% data, all N, M <= 10
For 40% data, all N, M <= 103
For 100% data, all 1 <= T <= 5, N, M <= 105, 0 <= K <= 3, 0 <= S, E <= 105.
Hint: HUGE input in this problem. Fast IO such as scanf and BufferedReader are recommended.
输出
For each test case, output a line with N numbers Ans1, Ans2, … , AnsN. Ansi is the number of times that the i-th module is started. In case the answers may be too large, output the answers modulo 142857 (the remainder of division by 142857).
样例输入
3
3 2
123 256
123 2 456 256
456 3 666 111 256
256 1 90
3 1
100
100 2 200 200
200 1 300
200 0
5 1
1
1 2 2 3
2 2 3 4
3 2 4 5
4 2 5 6
5 2 6 7
样例输出
1 1 3
1 2 2
1 1 2 3 5
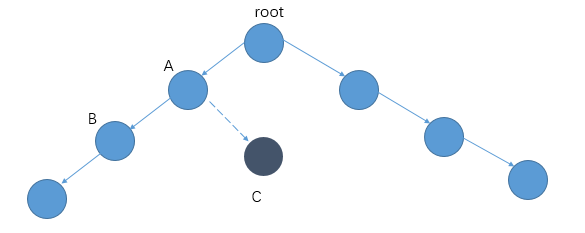
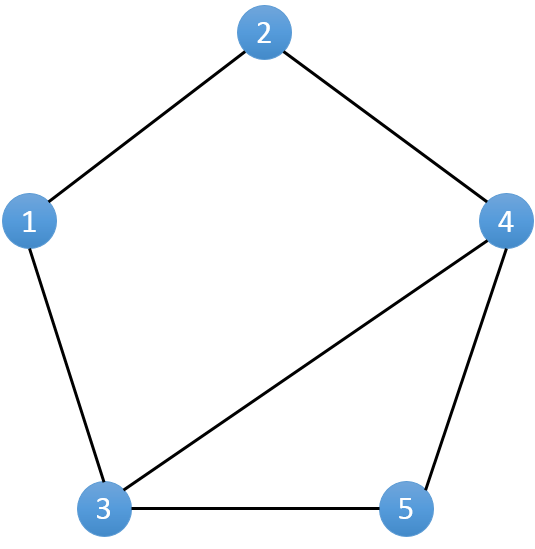 因为相亲总是在男女之间进行的,所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色,女性的节点染色黑色。对于得到的无向图来说,即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色,则表示这一条边所表示的记录有误。由于我们并不知道每个人的性别,我们的问题就转化为判定是否存在一个合理的染色方案,使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。那么,我们不妨将所有的点初始为未染色的状态。随机选择一个点,将其染成白色。再以它为起点,将所有相邻的点染成黑色。再以这些黑色的点为起点,将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图)
因为相亲总是在男女之间进行的,所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色,女性的节点染色黑色。对于得到的无向图来说,即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色,则表示这一条边所表示的记录有误。由于我们并不知道每个人的性别,我们的问题就转化为判定是否存在一个合理的染色方案,使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。那么,我们不妨将所有的点初始为未染色的状态。随机选择一个点,将其染成白色。再以它为起点,将所有相邻的点染成黑色。再以这些黑色的点为起点,将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图) 在染色的过程中,我们应该怎样发现错误的记录呢?相信你一定发现了吧。对于一个已经染色的点,如果存在一个与它相邻的已染色点和它的颜色相同,那么就一定存在一条错误的记录。(如上图的4,5节点)到此我们就得到了整个图的算法:选取一个未染色的点u进行染色
遍历u的相邻节点v:若v未染色,则染色成与u不同的颜色,并对v重复第2步;若v已经染色,如果 u和v颜色相同,判定不可行退出遍历。
若所有节点均已染色,则判定可行。
接下来就动手写写吧!
输入
第1行:1个正整数T(1≤T≤10)
接下来T组数据,每组数据按照以下格式给出:
第1行:2个正整数N,M(1≤N≤10,000,1≤M≤40,000)
第2..M+1行:每行两个整数u,v表示u和v之间有一条边
输出
第1..T行:第i行表示第i组数据是否有误。如果是正确的数据输出”Correct”,否则输出”Wrong”
样例输入
2
5 5
1 2
1 3
3 4
5 2
1 5
5 5
1 2
1 3
3 4
5 2
3 5
样例输出
Wrong
Correct
在染色的过程中,我们应该怎样发现错误的记录呢?相信你一定发现了吧。对于一个已经染色的点,如果存在一个与它相邻的已染色点和它的颜色相同,那么就一定存在一条错误的记录。(如上图的4,5节点)到此我们就得到了整个图的算法:选取一个未染色的点u进行染色
遍历u的相邻节点v:若v未染色,则染色成与u不同的颜色,并对v重复第2步;若v已经染色,如果 u和v颜色相同,判定不可行退出遍历。
若所有节点均已染色,则判定可行。
接下来就动手写写吧!
输入
第1行:1个正整数T(1≤T≤10)
接下来T组数据,每组数据按照以下格式给出:
第1行:2个正整数N,M(1≤N≤10,000,1≤M≤40,000)
第2..M+1行:每行两个整数u,v表示u和v之间有一条边
输出
第1..T行:第i行表示第i组数据是否有误。如果是正确的数据输出”Correct”,否则输出”Wrong”
样例输入
2
5 5
1 2
1 3
3 4
5 2
1 5
5 5
1 2
1 3
3 4
5 2
3 5
样例输出
Wrong
Correct
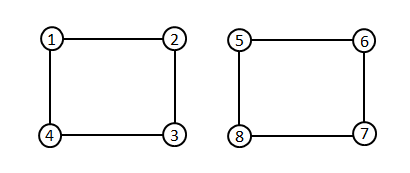 此图有两个连通分量,且两个分量都可以相亲成功,但如果只从第1点开始BFS,则不能遍历到第二个分量,导致失败。所以需要对每一个还未染色的点都开始BFS,如果都尝试过了还有点未染色,二分图判定失败;否则成功。
完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
int n, m;
vector<int> colored;
vector<vector<int>> path;
bool BFS(int start)
{
colored[start] = 0;
int num_colored = 1;
queue<int> point;
point.push(start);
while (!point.empty())
{
int current = point.front();
point.pop();
for (int i = 0; i < path[current].size(); i++)
{
if (colored[path[current][i]] == -1)
{
if (colored[current] == 0)
colored[path[current][i]] = 1;
else if (colored[current] == 1)
colored[path[current][i]] = 0;
num_colored++;
point.push(path[current][i]);
}
else if (colored[current] == colored[path[current][i]])
return false;
}
}
return true;
}
bool Check()
{
for (int i = 1; i <= n; i++)
if (colored[i] == -1)
if (!BFS(i))
return false;
return true;
}
int main()
{
int t,u,v;
scanf("%d", &t);
while (t–)
{
scanf("%d %d", &n, &m);
colored.clear();
colored.resize(n + 1, -1);
path.clear();
path.resize(n + 1);
for (int i = 0; i < m; i++)
{
scanf("%d %d", &u, &v);
path[u].push_back(v);
path[v].push_back(u);
}
if (Check())
printf("Correctn");
else
printf("Wrongn");
}
return 0;
}
[/cpp]
本代码提交AC,用时134MS,内存6MB。
]]>
此图有两个连通分量,且两个分量都可以相亲成功,但如果只从第1点开始BFS,则不能遍历到第二个分量,导致失败。所以需要对每一个还未染色的点都开始BFS,如果都尝试过了还有点未染色,二分图判定失败;否则成功。
完整代码如下:
[cpp]
#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
int n, m;
vector<int> colored;
vector<vector<int>> path;
bool BFS(int start)
{
colored[start] = 0;
int num_colored = 1;
queue<int> point;
point.push(start);
while (!point.empty())
{
int current = point.front();
point.pop();
for (int i = 0; i < path[current].size(); i++)
{
if (colored[path[current][i]] == -1)
{
if (colored[current] == 0)
colored[path[current][i]] = 1;
else if (colored[current] == 1)
colored[path[current][i]] = 0;
num_colored++;
point.push(path[current][i]);
}
else if (colored[current] == colored[path[current][i]])
return false;
}
}
return true;
}
bool Check()
{
for (int i = 1; i <= n; i++)
if (colored[i] == -1)
if (!BFS(i))
return false;
return true;
}
int main()
{
int t,u,v;
scanf("%d", &t);
while (t–)
{
scanf("%d %d", &n, &m);
colored.clear();
colored.resize(n + 1, -1);
path.clear();
path.resize(n + 1);
for (int i = 0; i < m; i++)
{
scanf("%d %d", &u, &v);
path[u].push_back(v);
path[v].push_back(u);
}
if (Check())
printf("Correctn");
else
printf("Wrongn");
}
return 0;
}
[/cpp]
本代码提交AC,用时134MS,内存6MB。
]]>
 Here “b” denotes pieces lying their black side up and “w” denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
Input
The input consists of 4 lines with 4 characters “w” or “b” each that denote game field position.
Output
Write to the output file a single integer number – the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it’s impossible to achieve the goal, then write the word “Impossible” (without quotes).
Sample Input
bwwb
bbwb
bwwb
bwww
Sample Output
4
Source
Northeastern Europe 2000
Here “b” denotes pieces lying their black side up and “w” denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
Input
The input consists of 4 lines with 4 characters “w” or “b” each that denote game field position.
Output
Write to the output file a single integer number – the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it’s impossible to achieve the goal, then write the word “Impossible” (without quotes).
Sample Input
bwwb
bbwb
bwwb
bwww
Sample Output
4
Source
Northeastern Europe 2000