POJ 2676-Sudoku
Sudoku
Time Limit: 2000MS Memory Limit: 65536K
Total Submissions: 14104 Accepted: 6963 Special Judge
Description
Sudoku is a very simple task. A square table with 9 rows and 9 columns is divided to 9 smaller squares 3×3 as shown on the Figure. In some of the cells are written decimal digits from 1 to 9. The other cells are empty. The goal is to fill the empty cells with decimal digits from 1 to 9, one digit per cell, in such way that in each row, in each column and in each marked 3×3 subsquare, all the digits from 1 to 9 to appear. Write a program to solve a given Sudoku-task.
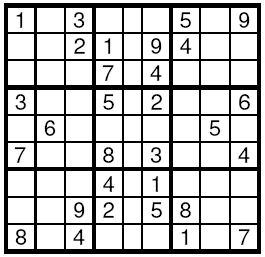 Input
The input data will start with the number of the test cases. For each test case, 9 lines follow, corresponding to the rows of the table. On each line a string of exactly 9 decimal digits is given, corresponding to the cells in this line. If a cell is empty it is represented by 0.
Output
For each test case your program should print the solution in the same format as the input data. The empty cells have to be filled according to the rules. If solutions is not unique, then the program may print any one of them.
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
Source
Southeastern Europe 2005
Input
The input data will start with the number of the test cases. For each test case, 9 lines follow, corresponding to the rows of the table. On each line a string of exactly 9 decimal digits is given, corresponding to the cells in this line. If a cell is empty it is represented by 0.
Output
For each test case your program should print the solution in the same format as the input data. The empty cells have to be filled according to the rules. If solutions is not unique, then the program may print any one of them.
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
Source
Southeastern Europe 2005
这一题是练习深度搜索和剪枝的好题目。题意很简答,数独游戏,在每一行、每一列和每一个小正方形填入1-9这9个数字,数字不能重复,求一种可以的方案。
因为只需要求一种可行解,根据
POJ Problem 3278: Catch That Cow后面的总结,很快有了深度搜索的思路:
从上到下,从左到右依次扫描每一个格子,如果这个格子上的数字不是0,说明原来就有数字了,不用填,测试下一个格子;如果这个格子为0,则求出可填入该格子的候选数字,再依次测试每一个候选数字是否可行,一直这样深度搜索下去,直到将所有格子测试完毕。这个思路相信很多人都能很快想到,完整的代码如下:
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int N=9;
int board[N][N];//棋盘
int candidates[N];//对于某一个坐标ij,可以填入的候选数字
//给定坐标(row,column),求它所在的小方格的左上角坐标
void get_subquare_start(int row,int column,int& x0,int& y0)
{
if(row<3&&column<3)
{
x0=0;
y0=0;
}
else if(row<3&&column<6)
{
x0=0;
y0=3;
}
else if(row<3&&column<9)
{
x0=0;
y0=6;
}
else if(row<6&&column<3)
{
x0=3;
y0=0;
}
else if(row<6&&column<6)
{
x0=3;
y0=3;
}
else if(row<6&&column<9)
{
x0=3;
y0=6;
}
else if(row<9&&column<3)
{
x0=6;
y0=0;
}
else if(row<9&&column<6)
{
x0=6;
y0=3;
}
else if(row<9&&column<9)
{
x0=6;
y0=6;
}
}
//给定坐标(row,column),将可以填入该坐标的候选数字放入vi
//思路就是先把candidates[N]填满1-9,然后将给定坐标的
//横轴、纵轴、小方格出现过的数字去掉,剩下的数字就是
//候选数字
void get_candidates(int row,int column,vector<int>& vi)
{
for(int i=0;i<N;i++)
candidates[i]=i+1;
for(int i=0;i<N;i++)//横轴
{
if(board[row][i]!=0)
candidates[board[row][i]-1]=0;
}
for(int i=0;i<N;i++)//纵轴
{
if(board[i][column]!=0)
candidates[board[i][column]-1]=0;
}
int x0,y0;
get_subquare_start(row,column,x0,y0);
for(int i=x0;i<x0+3;i++)//小方格
{
for(int j=y0;j<y0+3;j++)
{
if(board[i][j]!=0)
candidates[board[i][j]-1]=0;
}
}
for(int i=0;i<N;i++)//重复工作,可优化
if(candidates[i]!=0)
vi.push_back(candidates[i]);
}
//深度搜索
bool dfs(int pos)
{
if(pos==N*N)
{
return true;
}
int row=pos/N;
int column=pos%N;
if(board[row][column]!=0)//如果有数字
return dfs(pos+1);//则搜下一个格子
else
{
vector<int> local_candidates;//要使用局部的candidates,因为如果是全局的,那么回溯的时候candidates已经修改了
get_candidates(row,column,local_candidates);//获取可填入该格子的候选数字
int cand_num=local_candidates.size();
for(int i=0;i<cand_num;i++)
{
board[row][column]=local_candidates[i];//填入
if(dfs(pos+1))//继续搜下一个格子
return true;
}
board[row][column]=0;//回溯
return false;//回溯
}
}
int main()
{
freopen("input.txt","r",stdin);
int t;
char c;
cin>>t;
while(t–)
{
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
cin>>c;
board[i][j]=c-‘0’;
}
}
if(dfs(0))
{
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
cout<<board[i][j];
cout<<endl;
}
}
}
return 0;
}
[/cpp]
满心欢喜的提交后发现TLE超时了,此时泪流满面,后来又琢磨了一下,师兄给的分类是
简单搜索技巧和剪枝,我上面的代码压根就没有剪枝,TLE也就不足为奇了。
那么怎样剪枝?想一想我们手算解数独的过程,正常情况下,如果A这个格子有5个候选数字可以填入,而B这个格子只有2个候选数字可以填入,我们肯定会先填好B这个格子,再填A,因为B的情况少一些,而填完B之后,A的情况可能又会减少,这样比先填A再填B会快得多。根据这样的思路,我们
在每次深度搜索的时候,把每个空格的候选数字求出来,并求候选数字个数最少的那个格子C,填格子C,继续深度搜索,直到所有空格填满为止。
可能有的同学会问,每次深度搜索的时候都要求一遍
所有空格的候选数字,这样会不会耗时太多了,这个我也担心过,但是总体来说,剪枝比第一个版本的代码高效多了。下面是剪枝版本的完整代码:
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int N=9;
int board[N][N];//棋盘
int candidates[N];//对于某一个坐标ij,可以填入的候选数字
//给定坐标(row,column),求它所在的小方格的左上角坐标
void get_subquare_start(int row,int column,int& x0,int& y0)
{
if(row<3&&column<3)
{
x0=0;
y0=0;
}
else if(row<3&&column<6)
{
x0=0;
y0=3;
}
else if(row<3&&column<9)
{
x0=0;
y0=6;
}
else if(row<6&&column<3)
{
x0=3;
y0=0;
}
else if(row<6&&column<6)
{
x0=3;
y0=3;
}
else if(row<6&&column<9)
{
x0=3;
y0=6;
}
else if(row<9&&column<3)
{
x0=6;
y0=0;
}
else if(row<9&&column<6)
{
x0=6;
y0=3;
}
else if(row<9&&column<9)
{
x0=6;
y0=6;
}
}
//给定坐标(row,column),将可以填入该坐标的候选数字放入vi
//思路就是先把candidates[N]填满1-9,然后将给定坐标的
//横轴、纵轴、小方格出现过的数字去掉,剩下的数字就是
//候选数字
void get_candidates(int row,int column,vector<int>& vi)
{
for(int i=0;i<N;i++)
candidates[i]=i+1;
for(int i=0;i<N;i++)//横轴
{
if(board[row][i]!=0)
candidates[board[row][i]-1]=0;
}
for(int i=0;i<N;i++)//纵轴
{
if(board[i][column]!=0)
candidates[board[i][column]-1]=0;
}
int x0,y0;
get_subquare_start(row,column,x0,y0);
for(int i=x0;i<x0+3;i++)//小方格
{
for(int j=y0;j<y0+3;j++)
{
if(board[i][j]!=0)
candidates[board[i][j]-1]=0;
}
}
for(int i=0;i<N;i++)//重复工作,可优化
if(candidates[i]!=0)
vi.push_back(candidates[i]);
}
//深度搜索
bool dfs(vector<int>& blank_pos)
{
int blank_num=blank_pos.size();
if(blank_num==0)//如果空格都填完了,返回true
{
return true;
}
int row,column,pos;
int min_candidates=N+1;
vector<int> global_candidates;
for(int i=0;i<blank_num;i++)
{
row=blank_pos[i]/N;
column=blank_pos[i]%N;
vector<int> local_candidates;
get_candidates(row,column,local_candidates);//对于每一个空格求可填入的候选数字
if(local_candidates.size()<min_candidates)//求到最小值
{
pos=blank_pos[i];//记录位置
min_candidates=local_candidates.size();
global_candidates.clear();
global_candidates=local_candidates;//vector可以直接赋值
}
}
row=pos/N;
column=pos%N;
vector<int> next_blank_pos;
for(int j=0;j<blank_num;j++)
if(blank_pos[j]!=pos)
next_blank_pos.push_back(blank_pos[j]);//剩余的空格
for(int i=0;i<min_candidates;i++)
{
board[row][column]=global_candidates[i];//填入
if(dfs(next_blank_pos))//继续搜下一个格子
return true;
}
board[row][column]=0;//回溯
return false;//回溯
}
//剪枝版本,AC,用时282MS,内存240K
int main()
{
//freopen("input.txt","r",stdin);
int t;
char c;
cin>>t;
vector<int> blank_pos;
while(t–)
{
blank_pos.clear();//因为可能有多个case,所以每次都要clear!!!
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
cin>>c;
board[i][j]=c-‘0’;
if(board[i][j]==0)
blank_pos.push_back(i*N+j);
}
}
if(dfs(blank_pos))
{
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
cout<<board[i][j];
cout<<endl;
}
}
}
return 0;
}
[/cpp]
这个版本的代码需要注意一个小细节,我在每次输入的时候都将空格的位置记录在了blank_pos的vector中,因为题目说有多个case,所以每次输入的时候都要记得blank_pos.clear(),要不然会影响下一个case。这个版本的代码AC,用时282MS,内存240K。
AC之后,又看了一下discuss,发现很多同学谈到如果倒搜,会比顺搜快得多,倒搜就是从最后一个格子开始搜索。闲来无事,我就把第一个版本的代码改成了倒搜索,只需要修改两三个地方,代码如下:
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int N=9;
int board[N][N];//棋盘
int candidates[N];//对于某一个坐标ij,可以填入的候选数字
//给定坐标(row,column),求它所在的小方格的左上角坐标
void get_subquare_start(int row,int column,int& x0,int& y0)
{
if(row<3&&column<3)
{
x0=0;
y0=0;
}
else if(row<3&&column<6)
{
x0=0;
y0=3;
}
else if(row<3&&column<9)
{
x0=0;
y0=6;
}
else if(row<6&&column<3)
{
x0=3;
y0=0;
}
else if(row<6&&column<6)
{
x0=3;
y0=3;
}
else if(row<6&&column<9)
{
x0=3;
y0=6;
}
else if(row<9&&column<3)
{
x0=6;
y0=0;
}
else if(row<9&&column<6)
{
x0=6;
y0=3;
}
else if(row<9&&column<9)
{
x0=6;
y0=6;
}
}
//给定坐标(row,column),将可以填入该坐标的候选数字放入vi
//思路就是先把candidates[N]填满1-9,然后将给定坐标的
//横轴、纵轴、小方格出现过的数字去掉,剩下的数字就是
//候选数字
void get_candidates(int row,int column,vector<int>& vi)
{
for(int i=0;i<N;i++)
candidates[i]=i+1;
for(int i=0;i<N;i++)//横轴
{
if(board[row][i]!=0)
candidates[board[row][i]-1]=0;
}
for(int i=0;i<N;i++)//纵轴
{
if(board[i][column]!=0)
candidates[board[i][column]-1]=0;
}
int x0,y0;
get_subquare_start(row,column,x0,y0);
for(int i=x0;i<x0+3;i++)//小方格
{
for(int j=y0;j<y0+3;j++)
{
if(board[i][j]!=0)
candidates[board[i][j]-1]=0;
}
}
for(int i=0;i<N;i++)//重复工作,可优化
if(candidates[i]!=0)
vi.push_back(candidates[i]);
}
//深度搜索
bool dfs(int pos)
{
if(pos==-1)//倒搜到-1结束
{
return true;
}
int row=pos/N;
int column=pos%N;
if(board[row][column]!=0)//如果有数字
return dfs(pos-1);//则搜下一个格子
else
{
vector<int> local_candidates;//要使用局部的candidates,因为如果是全局的,那么回溯的时候candidates已经修改了
get_candidates(row,column,local_candidates);//获取可填入该格子的候选数字
int cand_num=local_candidates.size();
for(int i=0;i<cand_num;i++)
{
board[row][column]=local_candidates[i];//填入
if(dfs(pos-1))//继续搜下一个格子
return true;
}
board[row][column]=0;//回溯
return false;//回溯
}
}
//倒搜版本,AC,用时125MS,内存224K
int main()
{
//freopen("input.txt","r",stdin);
int t;
char c;
cin>>t;
while(t–)
{
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
cin>>c;
board[i][j]=c-‘0’;
}
}
if(dfs(N*N-1))//倒搜
{
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
cout<<board[i][j];
cout<<endl;
}
}
}
return 0;
}
[/cpp]
令我吃惊的是,倒搜这个版本的代码AC了,而且用时125MS,内存224K,居然比剪枝还要快,内存占用也更少。到现在我还没有搞清楚更快的原因。]]>
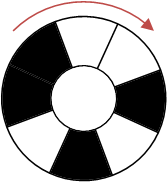 这个机关是一个圆环,一共有2^N个区域,每个区域都可以改变颜色,在黑白两种颜色之间切换。
小Ho控制主角在周围探索了一下,果然又发现了一个纸片:
机关黑色的部分表示为1,白色的部分表示为0,逆时针连续N个区域表示一个二进制数。打开机关的条件是合理调整圆环黑白两种颜色的分布,使得机关能够表示0~2^N-1所有的数字。
我尝试了很多次,终究没有办法打开,只得在此写下机关破解之法。
——By 无名的冒险者
小Ho:这什么意思啊?
小Hi:我给你举个例子,假如N=3,我们通过顺时针转动,可以使得正下方的3个区域表示为:
这个机关是一个圆环,一共有2^N个区域,每个区域都可以改变颜色,在黑白两种颜色之间切换。
小Ho控制主角在周围探索了一下,果然又发现了一个纸片:
机关黑色的部分表示为1,白色的部分表示为0,逆时针连续N个区域表示一个二进制数。打开机关的条件是合理调整圆环黑白两种颜色的分布,使得机关能够表示0~2^N-1所有的数字。
我尝试了很多次,终究没有办法打开,只得在此写下机关破解之法。
——By 无名的冒险者
小Ho:这什么意思啊?
小Hi:我给你举个例子,假如N=3,我们通过顺时针转动,可以使得正下方的3个区域表示为:
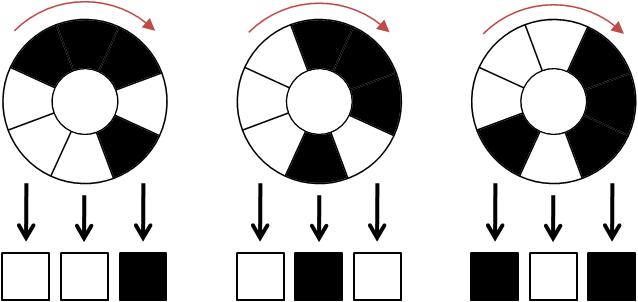 因为黑色表示为1,白色表示为0。则上面三个状态分别对应了二进制(001),(010),(101)
每转动一个区域,可以得到一个新的数字。一共可以转动2^N次,也就是2^N个数字。我们要调整黑白区域的位置,使得这2^N个数字恰好是0~2^N-1
小Ho:我懂了。若N=2,则将环上的黑白色块调整为”黑黑白白”,对应了”1100″。依次是”11″,”10″,”00″,”01″四个数字,正好是0~3。那么这个”黑黑白白”就可以打开机关了咯?
小Hi:我想应该是的。
小Ho:好像不是很难的样子,我来试试!
提示:有向图欧拉回路
输入
第1行:1个正整数,N。1≤N≤15
输出
第1行:1个长度为2^N的01串,表示一种符合要求的分布方案
样例输入
3
样例输出
00010111
因为黑色表示为1,白色表示为0。则上面三个状态分别对应了二进制(001),(010),(101)
每转动一个区域,可以得到一个新的数字。一共可以转动2^N次,也就是2^N个数字。我们要调整黑白区域的位置,使得这2^N个数字恰好是0~2^N-1
小Ho:我懂了。若N=2,则将环上的黑白色块调整为”黑黑白白”,对应了”1100″。依次是”11″,”10″,”00″,”01″四个数字,正好是0~3。那么这个”黑黑白白”就可以打开机关了咯?
小Hi:我想应该是的。
小Ho:好像不是很难的样子,我来试试!
提示:有向图欧拉回路
输入
第1行:1个正整数,N。1≤N≤15
输出
第1行:1个长度为2^N的01串,表示一种符合要求的分布方案
样例输入
3
样例输出
00010111
 主角继续往前走,面前出现了一座石桥,石桥的尽头有一道火焰墙,似乎无法通过。
小Hi注意到在桥头有一张小纸片,于是控制主角捡起了这张纸片,只见上面写着:
将M块骨牌首尾相连放置于石桥的凹糟中,即可关闭火焰墙。切记骨牌需要数字相同才能连接。
——By 无名的冒险者
小Hi和小Ho打开了主角的道具栏,发现主角恰好拥有M快骨牌。
小Ho:也就是说要把所有骨牌都放在凹槽中才能关闭火焰墙,数字相同是什么意思?
小Hi:你看,每一块骨牌两端各有一个数字,大概是只有当数字相同时才可以相连放置,比如:
主角继续往前走,面前出现了一座石桥,石桥的尽头有一道火焰墙,似乎无法通过。
小Hi注意到在桥头有一张小纸片,于是控制主角捡起了这张纸片,只见上面写着:
将M块骨牌首尾相连放置于石桥的凹糟中,即可关闭火焰墙。切记骨牌需要数字相同才能连接。
——By 无名的冒险者
小Hi和小Ho打开了主角的道具栏,发现主角恰好拥有M快骨牌。
小Ho:也就是说要把所有骨牌都放在凹槽中才能关闭火焰墙,数字相同是什么意思?
小Hi:你看,每一块骨牌两端各有一个数字,大概是只有当数字相同时才可以相连放置,比如:
 小Ho:原来如此,那么我们先看看能不能把所有的骨牌连接起来吧。
提示:Fleury算法求欧拉路径
输入
第1行:2个正整数,N,M。分别表示骨牌上出现的最大数字和骨牌数量。1≤N≤1,000,1≤M≤5,000
第2..M+1行:每行2个整数,u,v。第i+1行表示第i块骨牌两端的数字(u,v),1≤u,v≤N
输出
第1行:m+1个数字,表示骨牌首尾相连后的数字
比如骨牌连接的状态为(1,5)(5,3)(3,2)(2,4)(4,3),则输出”1 5 3 2 4 3″
你可以输出任意一组合法的解。
样例输入
5 5
3 5
3 2
4 2
3 4
5 1
样例输出
1 5 3 4 2 3
小Ho:原来如此,那么我们先看看能不能把所有的骨牌连接起来吧。
提示:Fleury算法求欧拉路径
输入
第1行:2个正整数,N,M。分别表示骨牌上出现的最大数字和骨牌数量。1≤N≤1,000,1≤M≤5,000
第2..M+1行:每行2个整数,u,v。第i+1行表示第i块骨牌两端的数字(u,v),1≤u,v≤N
输出
第1行:m+1个数字,表示骨牌首尾相连后的数字
比如骨牌连接的状态为(1,5)(5,3)(3,2)(2,4)(4,3),则输出”1 5 3 2 4 3″
你可以输出任意一组合法的解。
样例输入
5 5
3 5
3 2
4 2
3 4
5 1
样例输出
1 5 3 4 2 3
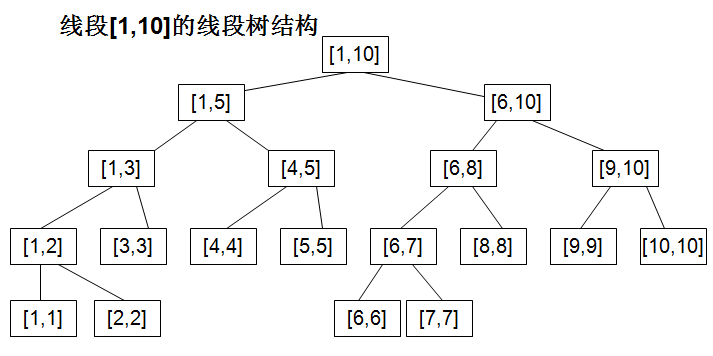 从图中可以看到构造线段树的过程就是一个二分的过程,不断将区间分成两半,直到只有一个元素。图中的线段树每一个节点是一个区间[l,r],本题我稍微改造了一下,改成了数组int seg_tree[left][length],比如seg_tree[i][j]表示从下标i开始,长度为j的这样一个区间上的最小值,这样就可以利用线段树来解决RMQ问题了。比如改造后的线段树就成了下面的样子:
从图中可以看到构造线段树的过程就是一个二分的过程,不断将区间分成两半,直到只有一个元素。图中的线段树每一个节点是一个区间[l,r],本题我稍微改造了一下,改成了数组int seg_tree[left][length],比如seg_tree[i][j]表示从下标i开始,长度为j的这样一个区间上的最小值,这样就可以利用线段树来解决RMQ问题了。比如改造后的线段树就成了下面的样子:
 因为树形这种特殊的结构,我们可以用一个DFS来对树实现二分构造,当DFS到某个节点长度为1时,其最小值就是w[i]本身,在回溯到父节点时,父节那个区间的最小值又是所有子节点最小值中的最小值。因为树的总节点数大约为2*n,所以复杂度O(n)。
当需要查询区间[l,r]的最小值时,只需对数组seg_tree二分搜索。具体来说,假设我们搜索到了节点[s_l,s_len],如果r<(s_l+s_len/2),说明区间[l,r]全在[s_l,s_len]的左边,我们递归在[s_l,s_len/2]区间找;如果l>=(s_l+s_len/2),说明区间[l,r]全在[s_l,s_len]的右边,我们递归在[s_l+s_len/2,s_len-s_len/2]区间找;如果以上两者都不是,说明[l,r]跨界了,而且中点下标一定是s_l+s_len/2,所以我们分别在二两半区间找,然后求这两者的最小值。复杂度O(lgn)。
当需要更新某个下标为pos的值为value时,也是DFS查找线段树,直到找到叶子seg_tree[pos][1],更新它的值,以及所有我们在查找过程经过的父节点的值。复杂度O(lgn)。
所以线段是的性质使得无论是构造、查询、更新操作,复杂度都只要O(lgn),这就是题目中所说的把总的复杂度平均分配到不同操作:平衡乃和谐之理。
完整代码如下:
[cpp]
#include<iostream>
using namespace std;
const int MAX_N=1e4+2;
int w[MAX_N];//每个商品重量
int n,m;
int seg_tree[MAX_N][MAX_N];//seg_tree[i][j]:起点为i,长度为j的区间的最小值
inline int get_min(int a,int b)
{
return a<b?a:b;
}
//深度优先遍历以构造线段树
void dfs(int left,int length)
{
if(length==1)
{
seg_tree[left][1]=w[left];
return;
}
dfs(left,length/2);
dfs(left+length/2,length-length/2);
seg_tree[left][length]=get_min(seg_tree[left][length/2],seg_tree[left+length/2][length-length/2]);//取最小值
}
//在区间[s_left,s_len]搜索区间[left,length]的最小值
int search_min(int s_left,int s_len,int left,int length)
{
if((s_left==left)&&(s_len==length))
return seg_tree[s_left][s_len];
if((left+length-1)<(s_left+s_len/2))//全在左半部分
{
return search_min(s_left,s_len/2,left,length);
}
else if(left>=(s_left+s_len/2))//全在右半部分
{
return search_min(s_left+s_len/2,s_len-s_len/2,left,length);
}
else//左右分开搜索
{
int left_len=s_left+s_len/2-left;
int right_len=length-left_len;
int min_left=search_min(s_left,s_len/2,left,left_len);
int min_right=search_min(s_left+s_len/2,s_len-s_len/2,s_left+s_len/2,right_len);
return get_min(min_left,min_right);
}
}
//从区间[s_left,s_len]开始更新下标pos的值为value
void update(int s_left,int s_len,int pos,int value)
{
if((s_left==pos)&&(s_len==1))
{
seg_tree[s_left][1]=value;
return ;
}
int mid=s_left+s_len/2;
if(pos<mid)
update(s_left,s_len/2,pos,value);
else
update(mid,s_len-s_len/2,pos,value);
seg_tree[s_left][s_len]=get_min(seg_tree[s_left][s_len/2],seg_tree[mid][s_len-s_len/2]);//更新父节点
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
for(int i=1;i<=n;i++)
cin>>w[i];
dfs(1,n);
cin>>m;
int p,l,r;
for(int i=0;i<m;i++)
{
cin>>p>>l>>r;
if(p==0)//查询
{
cout<<search_min(1,n,l,r-l+1)<<endl;
}
else//修改
{
update(1,n,l,r);
}
}
return 0;
}
[/cpp]
本代码提交AC,用时151MS,内存42MB。
]]>
因为树形这种特殊的结构,我们可以用一个DFS来对树实现二分构造,当DFS到某个节点长度为1时,其最小值就是w[i]本身,在回溯到父节点时,父节那个区间的最小值又是所有子节点最小值中的最小值。因为树的总节点数大约为2*n,所以复杂度O(n)。
当需要查询区间[l,r]的最小值时,只需对数组seg_tree二分搜索。具体来说,假设我们搜索到了节点[s_l,s_len],如果r<(s_l+s_len/2),说明区间[l,r]全在[s_l,s_len]的左边,我们递归在[s_l,s_len/2]区间找;如果l>=(s_l+s_len/2),说明区间[l,r]全在[s_l,s_len]的右边,我们递归在[s_l+s_len/2,s_len-s_len/2]区间找;如果以上两者都不是,说明[l,r]跨界了,而且中点下标一定是s_l+s_len/2,所以我们分别在二两半区间找,然后求这两者的最小值。复杂度O(lgn)。
当需要更新某个下标为pos的值为value时,也是DFS查找线段树,直到找到叶子seg_tree[pos][1],更新它的值,以及所有我们在查找过程经过的父节点的值。复杂度O(lgn)。
所以线段是的性质使得无论是构造、查询、更新操作,复杂度都只要O(lgn),这就是题目中所说的把总的复杂度平均分配到不同操作:平衡乃和谐之理。
完整代码如下:
[cpp]
#include<iostream>
using namespace std;
const int MAX_N=1e4+2;
int w[MAX_N];//每个商品重量
int n,m;
int seg_tree[MAX_N][MAX_N];//seg_tree[i][j]:起点为i,长度为j的区间的最小值
inline int get_min(int a,int b)
{
return a<b?a:b;
}
//深度优先遍历以构造线段树
void dfs(int left,int length)
{
if(length==1)
{
seg_tree[left][1]=w[left];
return;
}
dfs(left,length/2);
dfs(left+length/2,length-length/2);
seg_tree[left][length]=get_min(seg_tree[left][length/2],seg_tree[left+length/2][length-length/2]);//取最小值
}
//在区间[s_left,s_len]搜索区间[left,length]的最小值
int search_min(int s_left,int s_len,int left,int length)
{
if((s_left==left)&&(s_len==length))
return seg_tree[s_left][s_len];
if((left+length-1)<(s_left+s_len/2))//全在左半部分
{
return search_min(s_left,s_len/2,left,length);
}
else if(left>=(s_left+s_len/2))//全在右半部分
{
return search_min(s_left+s_len/2,s_len-s_len/2,left,length);
}
else//左右分开搜索
{
int left_len=s_left+s_len/2-left;
int right_len=length-left_len;
int min_left=search_min(s_left,s_len/2,left,left_len);
int min_right=search_min(s_left+s_len/2,s_len-s_len/2,s_left+s_len/2,right_len);
return get_min(min_left,min_right);
}
}
//从区间[s_left,s_len]开始更新下标pos的值为value
void update(int s_left,int s_len,int pos,int value)
{
if((s_left==pos)&&(s_len==1))
{
seg_tree[s_left][1]=value;
return ;
}
int mid=s_left+s_len/2;
if(pos<mid)
update(s_left,s_len/2,pos,value);
else
update(mid,s_len-s_len/2,pos,value);
seg_tree[s_left][s_len]=get_min(seg_tree[s_left][s_len/2],seg_tree[mid][s_len-s_len/2]);//更新父节点
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
for(int i=1;i<=n;i++)
cin>>w[i];
dfs(1,n);
cin>>m;
int p,l,r;
for(int i=0;i<m;i++)
{
cin>>p>>l>>r;
if(p==0)//查询
{
cout<<search_min(1,n,l,r-l+1)<<endl;
}
else//修改
{
update(1,n,l,r);
}
}
return 0;
}
[/cpp]
本代码提交AC,用时151MS,内存42MB。
]]>
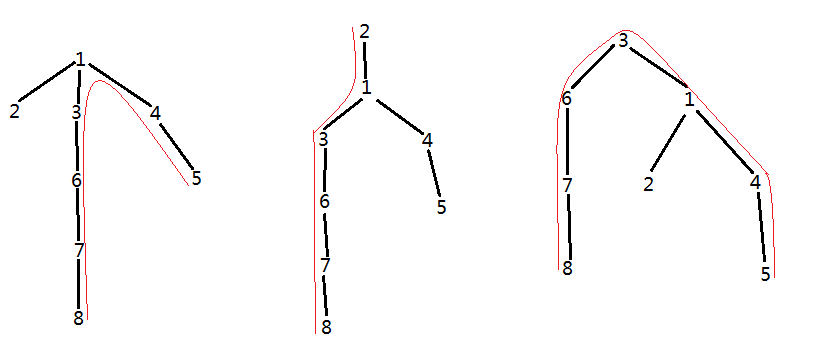 因为我们默认以t为根的树的最长路径一定经过节点t,所以上图最长路径分别为图中红色路线所示,长度分别为6,5,6(因为节点1和3都在最长路径上,所以他们求得的最长路径相等)。同理我们还可以求出以4,5…n为根(路径转折点)的最长路径,最后求这些最长路径中的最大值。
这个版本的代码如下:
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int MAX_N=1e5+2;
int n;//节点数
vector<vector<int> > f_s(MAX_N);//father-son和son-father关系,存储双边
vector<int> first,second;//first[i]和second[i]分别表示以i节点为根节点时(i节点以下构成的子树)的最大和次大长度
//参数分别为当前节点,父亲节点
void dfs(int root,int father)
{
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
if(f_s[root][i]!=father)//不能回溯
{
dfs(f_s[root][i],root);
if(first[f_s[root][i]]+1>first[root])
{
second[root]=first[root];
first[root]=first[f_s[root][i]]+1;
}
else if(first[f_s[root][i]]+1>second[root])
second[root]=first[f_s[root][i]]+1;
}
}
}
void init_first_second()
{
first.clear();
first.assign(n+1,0);
second.clear();
second.assign(n+1,0);
}
int main()
{
freopen("input.txt","r",stdin);
cin>>n;
int a,b;
for(int i=0;i<n-1;i++)
{
cin>>a>>b;
f_s[a].push_back(b);//记录双边关系
f_s[b].push_back(a);//记录双边关系
}
int ans=0;
for(int i=1;i<=n;i++)//枚举每一个节点为根节点(转折点)
{
init_first_second();
dfs(i,-1);
if(first[i]+second[i]>ans)
ans=first[i]+second[i];
}
cout<<ans;
return 0;
}
[/cpp]
但是很遗憾,提交后TLE。
后来我仔细想了想,无论我们从哪个点s开始对树DFS,我们求得的first[i]和second[i]都是以点i为根构成的子树中它的最长和次长距离,那么first[i]+second[i]不就代表了从i开始DFS时得到的最长距离吗?比如图中以2为根的树中,我们在DFS的过程中肯定已经求到了first[1]和second[1],然后才能求first[2]和second[2],而这里的first[1]和second[2]和图中以1为根时求得的first[1]和second[1]是完全一样的。而对于以3为根的树,因为3正好在最长路径上,所以这里的first[1]和second[1]要小于前面两种情况,但是first[3]+second[3]和前面两种情况的first[1]+second[1]是相等的。
说了这么多,不知道同学们有没有发现,不管从哪个点开始DFS,只要一遍DFS结束,最长路径总会出现在某个first[i]+second[i]中。
至此,可以省略上一个版本中的for循环,只要一个DFS即可:
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int MAX_N=1e5+2;
int n;//节点数
vector<vector<int> > f_s(MAX_N);//father-son和son-father关系,存储双边
vector<int> first,second;//first[i]和second[i]分别表示以i节点为根节点时(i节点以下构成的子树)的最大和次大长度
int longest=0;//最终结果
//参数分别为当前节点,父亲节点
void dfs(int root,int father)
{
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
if(f_s[root][i]!=father)//不能回溯
{
dfs(f_s[root][i],root);
if(first[f_s[root][i]]+1>first[root])//更新最大和次大
{
second[root]=first[root];
first[root]=first[f_s[root][i]]+1;
}
else if(first[f_s[root][i]]+1>second[root])//只更新次大
second[root]=first[f_s[root][i]]+1;
}
}
if(first[root]+second[root]>longest)//更新全局最大
longest=first[root]+second[root];
}
void init_first_second()
{
first.assign(n+1,0);
second.assign(n+1,0);
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
int a,b;
for(int i=0;i<n-1;i++)
{
cin>>a>>b;
f_s[a].push_back(b);//记录双边关系
f_s[b].push_back(a);//记录双边关系
}
init_first_second();
dfs(1,-1);//使用任意一个节点DFS,结果都是一样的。
/*int ans=0;
for(int i=1;i<=n;i++)//该循环可在DFS时完成
{
if(first[i]+second[i]>ans)
ans=first[i]+second[i];
}*/
cout<<longest;
return 0;
}
[/cpp]
本代码提交AC,用时224MS,内存9MB。
第二种方法不太好理解,所以还是建议大家用第一种方法。
网上关于树的直径介绍了3种方法,可以参考
因为我们默认以t为根的树的最长路径一定经过节点t,所以上图最长路径分别为图中红色路线所示,长度分别为6,5,6(因为节点1和3都在最长路径上,所以他们求得的最长路径相等)。同理我们还可以求出以4,5…n为根(路径转折点)的最长路径,最后求这些最长路径中的最大值。
这个版本的代码如下:
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int MAX_N=1e5+2;
int n;//节点数
vector<vector<int> > f_s(MAX_N);//father-son和son-father关系,存储双边
vector<int> first,second;//first[i]和second[i]分别表示以i节点为根节点时(i节点以下构成的子树)的最大和次大长度
//参数分别为当前节点,父亲节点
void dfs(int root,int father)
{
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
if(f_s[root][i]!=father)//不能回溯
{
dfs(f_s[root][i],root);
if(first[f_s[root][i]]+1>first[root])
{
second[root]=first[root];
first[root]=first[f_s[root][i]]+1;
}
else if(first[f_s[root][i]]+1>second[root])
second[root]=first[f_s[root][i]]+1;
}
}
}
void init_first_second()
{
first.clear();
first.assign(n+1,0);
second.clear();
second.assign(n+1,0);
}
int main()
{
freopen("input.txt","r",stdin);
cin>>n;
int a,b;
for(int i=0;i<n-1;i++)
{
cin>>a>>b;
f_s[a].push_back(b);//记录双边关系
f_s[b].push_back(a);//记录双边关系
}
int ans=0;
for(int i=1;i<=n;i++)//枚举每一个节点为根节点(转折点)
{
init_first_second();
dfs(i,-1);
if(first[i]+second[i]>ans)
ans=first[i]+second[i];
}
cout<<ans;
return 0;
}
[/cpp]
但是很遗憾,提交后TLE。
后来我仔细想了想,无论我们从哪个点s开始对树DFS,我们求得的first[i]和second[i]都是以点i为根构成的子树中它的最长和次长距离,那么first[i]+second[i]不就代表了从i开始DFS时得到的最长距离吗?比如图中以2为根的树中,我们在DFS的过程中肯定已经求到了first[1]和second[1],然后才能求first[2]和second[2],而这里的first[1]和second[2]和图中以1为根时求得的first[1]和second[1]是完全一样的。而对于以3为根的树,因为3正好在最长路径上,所以这里的first[1]和second[1]要小于前面两种情况,但是first[3]+second[3]和前面两种情况的first[1]+second[1]是相等的。
说了这么多,不知道同学们有没有发现,不管从哪个点开始DFS,只要一遍DFS结束,最长路径总会出现在某个first[i]+second[i]中。
至此,可以省略上一个版本中的for循环,只要一个DFS即可:
[cpp]
#include<iostream>
#include<vector>
using namespace std;
const int MAX_N=1e5+2;
int n;//节点数
vector<vector<int> > f_s(MAX_N);//father-son和son-father关系,存储双边
vector<int> first,second;//first[i]和second[i]分别表示以i节点为根节点时(i节点以下构成的子树)的最大和次大长度
int longest=0;//最终结果
//参数分别为当前节点,父亲节点
void dfs(int root,int father)
{
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
if(f_s[root][i]!=father)//不能回溯
{
dfs(f_s[root][i],root);
if(first[f_s[root][i]]+1>first[root])//更新最大和次大
{
second[root]=first[root];
first[root]=first[f_s[root][i]]+1;
}
else if(first[f_s[root][i]]+1>second[root])//只更新次大
second[root]=first[f_s[root][i]]+1;
}
}
if(first[root]+second[root]>longest)//更新全局最大
longest=first[root]+second[root];
}
void init_first_second()
{
first.assign(n+1,0);
second.assign(n+1,0);
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
int a,b;
for(int i=0;i<n-1;i++)
{
cin>>a>>b;
f_s[a].push_back(b);//记录双边关系
f_s[b].push_back(a);//记录双边关系
}
init_first_second();
dfs(1,-1);//使用任意一个节点DFS,结果都是一样的。
/*int ans=0;
for(int i=1;i<=n;i++)//该循环可在DFS时完成
{
if(first[i]+second[i]>ans)
ans=first[i]+second[i];
}*/
cout<<longest;
return 0;
}
[/cpp]
本代码提交AC,用时224MS,内存9MB。
第二种方法不太好理解,所以还是建议大家用第一种方法。
网上关于树的直径介绍了3种方法,可以参考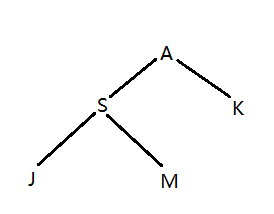 是样例输入构成的一个家谱树,我们常规DFS这个树的序列是这样的:ASJMK。但是本题在进入和离开某个节点时都需要记录下来,而且每访问完一个子节点,要访问下一个子节点时,也需要记录当前父节点。比如访问完J准备访问M时,需要记录S,由此形成的序列为:ASJSMSAKA。
DFS生成的数组B长度大概为边数的两倍,所以复杂度级别只是O(n)的。
DFS之后就把树转换为了数组B[],因为使用RMQ-ST算法需要求某个区间的最小深度节点,所以在DFS的时候还需要记录每个节点的深度信息,而且还要记录每个节点最后访问的下标,这两点都不难,大家直接看代码即可。
RMQ-ST算法
得到数组B后就好办了,可以利用昨天学习的RMQ-ST算法求解2的幂区间长度间深度最小的节点,不过因为我们这题最终输出的是节点的名字而不是节点的深度,所以RMQ-ST比较的是深度,但存储的是节点名。
观察RMQ-ST算法的二重循环知道其复杂度为O(nlgn)。
在线求解
一切准备就绪后就可以求解了,首先根据字符串名字找到对应数字序号,然后查看两节点最后出现在树中的下标l,r,再讲[l,r]区间分成能覆盖[l,r]的2的幂的长度的半区间[l,t]和[t+1,r],最后求这两个区间最小深度的节点,输出其名称。
完整代码如下:
[cpp]
#include<iostream>
#include<map>
#include<string>
#include<vector>
#include<cmath>
using namespace std;
const int MAX_N=100010;//最大人数
map<string,int> name_index;//名字转换为数字
vector<string> index_name(MAX_N);//数字转换为名字
int n,m,k;//k全部记录将树转换成数组tree[]是的下标,转换结束时k即为tree[]的长度
vector<vector<int> > f_s(MAX_N);//f_s[i]表示第i个父亲的所有孩子
int tree[2*MAX_N];//DFS将树转换为的数组
int depth[MAX_N];//每个点在树中的深度
int rmq[MAX_N][30];//区间深度最低值
int last_show[MAX_N];//某个元素最后出现在tree中的位置(下标)
//保存某个人的信息,并返回其下标
int store_name(string name)
{
map<string,int>::iterator it=name_index.find(name);
if(it==name_index.end())//还不存在
{
int curr_index=name_index.size();//用当前已有人数作为其下标,正好是递增的。
name_index.insert(make_pair(name,curr_index));
index_name[curr_index]=name;//记录
return curr_index;//返回下标
}
else
return it->second;//已经存在,直接返回
}
//深度遍历树
void DFS(int root,int deep)
{
tree[k++]=root;//进入即记录
depth[root]=deep;//记录深度
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
DFS(f_s[root][i],deep+1);
tree[k++]=root;//每返回一次都要记录一次根节点
}
last_show[root]=k-1;//root节点最后出现的位置
}
//求a,b最小值
inline int get_min(int a,int b)
{
return a<b?a:b;
}
void init_rmq()
{
for(int j=0;j<k;j++)
//rmq[j][0]=depth[tree[j]];
rmq[j][0]=tree[j];//保存的是这个节点,而不是它的深度,方便最后输出
int q=floor(log((double)k)/log(2.0));
for(int i=1;i<=q;i++)
{
for(int j=k-1;j>=0;j–)
{
rmq[j][i]=rmq[j][i-1];
if(j+(1<<(i-1))<k)
{
if(depth[rmq[j+(1<<(i-1))][i-1]]<depth[rmq[j][i]])//+优先级高于<<,所以改j+1<<(i-1)为j+(1<<(i-1))
rmq[j][i]=rmq[j+(1<<(i-1))][i-1];
}
//rmq[j][i]=get_min(rmq[j][i],rmq[j+1<<(i-1)][i-1]);
}
}
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
string name1,name2;
int index1,index2;
while(n–)
{
cin>>name1>>name2;
index1=store_name(name1);
index2=store_name(name2);
f_s[index1].push_back(index2);
}
k=0;//开始时树的下标为0,DFS完之后正好是tree[]数组的长度,可以作为rmq-st的n
DFS(0,0);
init_rmq();
cin>>m;
int l,r,t;
while(m–)
{
cin>>name1>>name2;
if(name1==name2)
{
cout<<name1<<endl;
continue;
}
index1=store_name(name1);
index2=store_name(name2);
l=last_show[index1];
r=last_show[index2];
if(l>r)//保证l<=r
{
int tmp=r;
r=l;
l=tmp;
}
t=floor(log(double(r-l+1))/log(2.0));//找到能使[l,r]分为两半的指数
cout<<index_name[get_min(rmq[l][t],rmq[r-(1<<t)+1][t])]<<endl;//r-(1<<t)+1,记得+1
}
return 0;
}
[/cpp]
本代码提交AC,用时202MS,内存8MB。
相比于
是样例输入构成的一个家谱树,我们常规DFS这个树的序列是这样的:ASJMK。但是本题在进入和离开某个节点时都需要记录下来,而且每访问完一个子节点,要访问下一个子节点时,也需要记录当前父节点。比如访问完J准备访问M时,需要记录S,由此形成的序列为:ASJSMSAKA。
DFS生成的数组B长度大概为边数的两倍,所以复杂度级别只是O(n)的。
DFS之后就把树转换为了数组B[],因为使用RMQ-ST算法需要求某个区间的最小深度节点,所以在DFS的时候还需要记录每个节点的深度信息,而且还要记录每个节点最后访问的下标,这两点都不难,大家直接看代码即可。
RMQ-ST算法
得到数组B后就好办了,可以利用昨天学习的RMQ-ST算法求解2的幂区间长度间深度最小的节点,不过因为我们这题最终输出的是节点的名字而不是节点的深度,所以RMQ-ST比较的是深度,但存储的是节点名。
观察RMQ-ST算法的二重循环知道其复杂度为O(nlgn)。
在线求解
一切准备就绪后就可以求解了,首先根据字符串名字找到对应数字序号,然后查看两节点最后出现在树中的下标l,r,再讲[l,r]区间分成能覆盖[l,r]的2的幂的长度的半区间[l,t]和[t+1,r],最后求这两个区间最小深度的节点,输出其名称。
完整代码如下:
[cpp]
#include<iostream>
#include<map>
#include<string>
#include<vector>
#include<cmath>
using namespace std;
const int MAX_N=100010;//最大人数
map<string,int> name_index;//名字转换为数字
vector<string> index_name(MAX_N);//数字转换为名字
int n,m,k;//k全部记录将树转换成数组tree[]是的下标,转换结束时k即为tree[]的长度
vector<vector<int> > f_s(MAX_N);//f_s[i]表示第i个父亲的所有孩子
int tree[2*MAX_N];//DFS将树转换为的数组
int depth[MAX_N];//每个点在树中的深度
int rmq[MAX_N][30];//区间深度最低值
int last_show[MAX_N];//某个元素最后出现在tree中的位置(下标)
//保存某个人的信息,并返回其下标
int store_name(string name)
{
map<string,int>::iterator it=name_index.find(name);
if(it==name_index.end())//还不存在
{
int curr_index=name_index.size();//用当前已有人数作为其下标,正好是递增的。
name_index.insert(make_pair(name,curr_index));
index_name[curr_index]=name;//记录
return curr_index;//返回下标
}
else
return it->second;//已经存在,直接返回
}
//深度遍历树
void DFS(int root,int deep)
{
tree[k++]=root;//进入即记录
depth[root]=deep;//记录深度
int sons=f_s[root].size();
for(int i=0;i<sons;i++)
{
DFS(f_s[root][i],deep+1);
tree[k++]=root;//每返回一次都要记录一次根节点
}
last_show[root]=k-1;//root节点最后出现的位置
}
//求a,b最小值
inline int get_min(int a,int b)
{
return a<b?a:b;
}
void init_rmq()
{
for(int j=0;j<k;j++)
//rmq[j][0]=depth[tree[j]];
rmq[j][0]=tree[j];//保存的是这个节点,而不是它的深度,方便最后输出
int q=floor(log((double)k)/log(2.0));
for(int i=1;i<=q;i++)
{
for(int j=k-1;j>=0;j–)
{
rmq[j][i]=rmq[j][i-1];
if(j+(1<<(i-1))<k)
{
if(depth[rmq[j+(1<<(i-1))][i-1]]<depth[rmq[j][i]])//+优先级高于<<,所以改j+1<<(i-1)为j+(1<<(i-1))
rmq[j][i]=rmq[j+(1<<(i-1))][i-1];
}
//rmq[j][i]=get_min(rmq[j][i],rmq[j+1<<(i-1)][i-1]);
}
}
}
int main()
{
//freopen("input.txt","r",stdin);
cin>>n;
string name1,name2;
int index1,index2;
while(n–)
{
cin>>name1>>name2;
index1=store_name(name1);
index2=store_name(name2);
f_s[index1].push_back(index2);
}
k=0;//开始时树的下标为0,DFS完之后正好是tree[]数组的长度,可以作为rmq-st的n
DFS(0,0);
init_rmq();
cin>>m;
int l,r,t;
while(m–)
{
cin>>name1>>name2;
if(name1==name2)
{
cout<<name1<<endl;
continue;
}
index1=store_name(name1);
index2=store_name(name2);
l=last_show[index1];
r=last_show[index2];
if(l>r)//保证l<=r
{
int tmp=r;
r=l;
l=tmp;
}
t=floor(log(double(r-l+1))/log(2.0));//找到能使[l,r]分为两半的指数
cout<<index_name[get_min(rmq[l][t],rmq[r-(1<<t)+1][t])]<<endl;//r-(1<<t)+1,记得+1
}
return 0;
}
[/cpp]
本代码提交AC,用时202MS,内存8MB。
相比于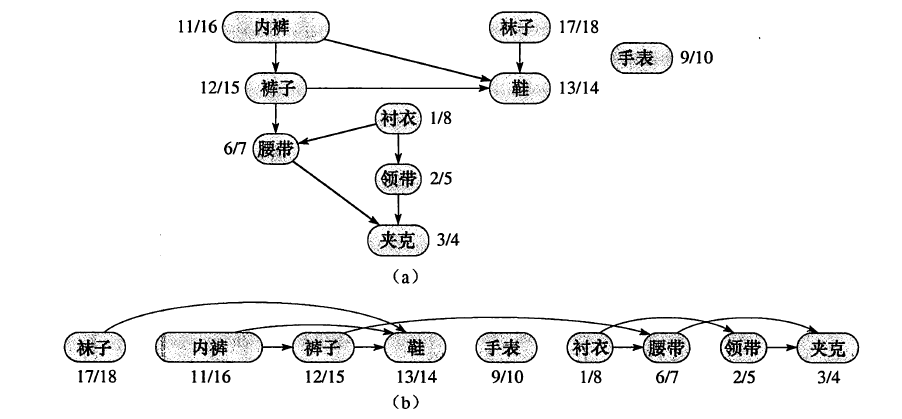 如上图是《算法导论》中关于拓扑排序的一个例子,这是某位教授起床后需要穿戴衣物的顺序,比如只有先穿了袜子才能穿鞋、但是穿鞋和戴手表并没有严格的先后顺序。拓扑排序的功能就是根据图(a)的拓扑图,得到图(b)中节点的先后顺序。
常见的拓扑排序算法有两种:Kahn算法和基于DFS的算法,这两种算法都很好理解,详细的解释请看维基百科
如上图是《算法导论》中关于拓扑排序的一个例子,这是某位教授起床后需要穿戴衣物的顺序,比如只有先穿了袜子才能穿鞋、但是穿鞋和戴手表并没有严格的先后顺序。拓扑排序的功能就是根据图(a)的拓扑图,得到图(b)中节点的先后顺序。
常见的拓扑排序算法有两种:Kahn算法和基于DFS的算法,这两种算法都很好理解,详细的解释请看维基百科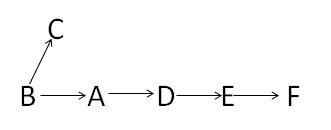 那么怎么判断生产的拓扑序列是否是严格的有序序列呢?基本原则就是就是任意取序列中的两个点,看能不能比较大小,如果能则是严格有序,否则不是。
我起初想到的是对拓扑序列的第一个节点进行深度遍历,遍历之后如果所有的节点都访问了,那么这是一个严格有序的序列,否则不是。后来证明这是不正确的,比如上图从B点开始DFS,遍历完F之后回溯到B点再访问C点,这样即使它不是严格有序的,但DFS还是访问了所有节点。
后来想到了Floyd算法。对拓扑图进行Floyd算法之后,会得到任意两点之间的最短距离。如果拓扑序列中前面的节点都可以到达后面的节点(最短距离不为无穷),则是严格有序的;否则不是。比如上图的一个拓扑序列为BCADEF(不唯一,还可以是BADEFC),但是C到ADEF的最短距离都是无穷,所以这个序列不是严格有序的。
把这些大的问题搞清楚之后就可以写代码了,一些小细节可以看我代码里的注释。
[cpp]
#include<iostream>
//#include<set>
#include<list>
#include<string>
#include<vector>
using namespace std;
int n,m;
const int MAX_N=26;
const int MAX_DIS=10000;
//*******这些都是维基百科关于拓扑排序(DFS版)里的变量含义
int temporary[MAX_N];
int permanent[MAX_N];
int marked[MAX_N];
//*******************************
int path[MAX_N][MAX_N];
//int dfs_visited[MAX_N];
list<int> L;//拓扑排序生产的顺序链
bool isDAG;//DAG=directed acyclic graph,无回路有向图
//每一个测试用例都要初始化路径
void init_path()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
path[i][j]=0;
}
//每一次拓扑排序都要初始化temporary,permanent,marked
void init_tpm()
{
isDAG=true;
L.clear();
for(int i=0;i<n;i++)
{
temporary[i]=0;
permanent[i]=0;
marked[i]=0;
}
}
//递归访问。具体看维基百科
void visit(int i)
{
if(temporary[i]==1)
{
isDAG=false;
return;
}
else
{
if(marked[i]==0)
{
marked[i]=1;
temporary[i]=1;
for(int j=0;j<n;j++)
{
if(path[i][j]==1)
{
visit(j);
}
}
permanent[i]=1;
temporary[i]=0;
L.push_front(i);
}
}
}
/*
void init_dfs()
{
for(int i=0;i<n;i++)
dfs_visited[i]=0;
}*/
/*
//DFS有缺陷
void DFS(int v)
{
if(dfs_visited[v]==0)
{
dfs_visited[v]=1;
for(int i=0;i<n;i++)
{
if(dfs_visited[i]==0&&path[v][i]==1)
{
DFS(i);
}
}
}
}*/
//使用Floyd算法来判断生产的拓扑排序是否是严格有序的
bool Floyd()
{
int copy_path[MAX_N][MAX_N];
for(int i=0;i<n;i++)//首先复制一份路径图
for(int j=0;j<n;j++)
{
copy_path[i][j]=path[i][j];
if(i!=j&©_path[i][j]==0)//如果原来两点距离为0,说明他们是不直接连通的
copy_path[i][j]=MAX_DIS;//置为无穷
}
//floyd算法
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++) if(copy_path[i][j]>copy_path[i][k]+copy_path[k][j])
copy_path[i][j]=copy_path[i][k]+copy_path[k][j];
vector<int> seq;//把原来用链表的拓扑序列转换成数组,方便后面的操作
list<int>::iterator it=L.begin();
while(it!=L.end())
{
seq.push_back(*it);
it++;
}
//如果这个拓扑链是严格有序的话,则前面的元素到后面的元素一定是可达的。
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++) { if(copy_path[seq[i]][seq[j]]>=MAX_DIS)//如果不可达,则不是严格有序的。
return false;
}
}
return true;
}
//拓扑排序DFS版本。返回0:有回路;1:虽然是拓扑排序,但非连通(不是严格有序);2:是拓扑排序且连通(严格有序)(即任意两个元素都可以比较大小)
int topological_sorting()
{
for(int i=0;i<n;i++)
{
if(marked[i]==0)
{
visit(i);
}
}
if(!isDAG)
return 0;
else
{
/*init_dfs();
DFS(*L.begin());
for(int i=0;i<n;i++) { if(dfs_visited[i]==0) { return 1; } }*/ if(Floyd()) return 2; else return 1; } } int main() { //freopen("input.txt","r",stdin); string tmp; while(cin>>n>>m&&n&&m)
{
init_path();
vector<string> relations(m);
int i;
for(i=0;i<m;i++)//一次性把所有输入都存起来,免得后续麻烦 { cin>>relations[i];
}
int rs=-1;
for(i=0;i<m;i++)//每增加一个关系,都要重新拓扑排序一次
{
init_tpm();//每次都要初始化
tmp=relations[i];
path[tmp[0]-‘A’][tmp[2]-‘A’]=1;
rs=topological_sorting();
if(rs==0)
{
cout<<"Inconsistency found after "<<i+1<<" relations."<<endl;
break;//如果是回路的话,后续的输入可以跳过
}
else if(rs==2)//成功
{
cout<<"Sorted sequence determined after "<<i+1<<" relations: ";
list<int>::iterator it=L.begin();
while(it!=L.end())
{
char c=’A’+*it;
cout<<c;
it++;
}
cout<<"."<<endl;
break;//后续输入跳过
}
}
if(i==m&&rs==1)//如果处理完所有输入都没有形成严格有序的拓扑序列
cout<<"Sorted sequence cannot be determined."<<endl;
}
return 0;
}
[/cpp]
我原本以为又是DFS,又是Floyd,算法时空效率会很低,但是提交后AC,用时125MS,内存244K,也不是很差。
代码中的拓扑排序算法使用的是基于DFS的版本,大家也可以改成Kahn算法。
如果觉得自己的代码是对的,但是提交WA的,可以使用这两个测试数据:
那么怎么判断生产的拓扑序列是否是严格的有序序列呢?基本原则就是就是任意取序列中的两个点,看能不能比较大小,如果能则是严格有序,否则不是。
我起初想到的是对拓扑序列的第一个节点进行深度遍历,遍历之后如果所有的节点都访问了,那么这是一个严格有序的序列,否则不是。后来证明这是不正确的,比如上图从B点开始DFS,遍历完F之后回溯到B点再访问C点,这样即使它不是严格有序的,但DFS还是访问了所有节点。
后来想到了Floyd算法。对拓扑图进行Floyd算法之后,会得到任意两点之间的最短距离。如果拓扑序列中前面的节点都可以到达后面的节点(最短距离不为无穷),则是严格有序的;否则不是。比如上图的一个拓扑序列为BCADEF(不唯一,还可以是BADEFC),但是C到ADEF的最短距离都是无穷,所以这个序列不是严格有序的。
把这些大的问题搞清楚之后就可以写代码了,一些小细节可以看我代码里的注释。
[cpp]
#include<iostream>
//#include<set>
#include<list>
#include<string>
#include<vector>
using namespace std;
int n,m;
const int MAX_N=26;
const int MAX_DIS=10000;
//*******这些都是维基百科关于拓扑排序(DFS版)里的变量含义
int temporary[MAX_N];
int permanent[MAX_N];
int marked[MAX_N];
//*******************************
int path[MAX_N][MAX_N];
//int dfs_visited[MAX_N];
list<int> L;//拓扑排序生产的顺序链
bool isDAG;//DAG=directed acyclic graph,无回路有向图
//每一个测试用例都要初始化路径
void init_path()
{
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
path[i][j]=0;
}
//每一次拓扑排序都要初始化temporary,permanent,marked
void init_tpm()
{
isDAG=true;
L.clear();
for(int i=0;i<n;i++)
{
temporary[i]=0;
permanent[i]=0;
marked[i]=0;
}
}
//递归访问。具体看维基百科
void visit(int i)
{
if(temporary[i]==1)
{
isDAG=false;
return;
}
else
{
if(marked[i]==0)
{
marked[i]=1;
temporary[i]=1;
for(int j=0;j<n;j++)
{
if(path[i][j]==1)
{
visit(j);
}
}
permanent[i]=1;
temporary[i]=0;
L.push_front(i);
}
}
}
/*
void init_dfs()
{
for(int i=0;i<n;i++)
dfs_visited[i]=0;
}*/
/*
//DFS有缺陷
void DFS(int v)
{
if(dfs_visited[v]==0)
{
dfs_visited[v]=1;
for(int i=0;i<n;i++)
{
if(dfs_visited[i]==0&&path[v][i]==1)
{
DFS(i);
}
}
}
}*/
//使用Floyd算法来判断生产的拓扑排序是否是严格有序的
bool Floyd()
{
int copy_path[MAX_N][MAX_N];
for(int i=0;i<n;i++)//首先复制一份路径图
for(int j=0;j<n;j++)
{
copy_path[i][j]=path[i][j];
if(i!=j&©_path[i][j]==0)//如果原来两点距离为0,说明他们是不直接连通的
copy_path[i][j]=MAX_DIS;//置为无穷
}
//floyd算法
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++) if(copy_path[i][j]>copy_path[i][k]+copy_path[k][j])
copy_path[i][j]=copy_path[i][k]+copy_path[k][j];
vector<int> seq;//把原来用链表的拓扑序列转换成数组,方便后面的操作
list<int>::iterator it=L.begin();
while(it!=L.end())
{
seq.push_back(*it);
it++;
}
//如果这个拓扑链是严格有序的话,则前面的元素到后面的元素一定是可达的。
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++) { if(copy_path[seq[i]][seq[j]]>=MAX_DIS)//如果不可达,则不是严格有序的。
return false;
}
}
return true;
}
//拓扑排序DFS版本。返回0:有回路;1:虽然是拓扑排序,但非连通(不是严格有序);2:是拓扑排序且连通(严格有序)(即任意两个元素都可以比较大小)
int topological_sorting()
{
for(int i=0;i<n;i++)
{
if(marked[i]==0)
{
visit(i);
}
}
if(!isDAG)
return 0;
else
{
/*init_dfs();
DFS(*L.begin());
for(int i=0;i<n;i++) { if(dfs_visited[i]==0) { return 1; } }*/ if(Floyd()) return 2; else return 1; } } int main() { //freopen("input.txt","r",stdin); string tmp; while(cin>>n>>m&&n&&m)
{
init_path();
vector<string> relations(m);
int i;
for(i=0;i<m;i++)//一次性把所有输入都存起来,免得后续麻烦 { cin>>relations[i];
}
int rs=-1;
for(i=0;i<m;i++)//每增加一个关系,都要重新拓扑排序一次
{
init_tpm();//每次都要初始化
tmp=relations[i];
path[tmp[0]-‘A’][tmp[2]-‘A’]=1;
rs=topological_sorting();
if(rs==0)
{
cout<<"Inconsistency found after "<<i+1<<" relations."<<endl;
break;//如果是回路的话,后续的输入可以跳过
}
else if(rs==2)//成功
{
cout<<"Sorted sequence determined after "<<i+1<<" relations: ";
list<int>::iterator it=L.begin();
while(it!=L.end())
{
char c=’A’+*it;
cout<<c;
it++;
}
cout<<"."<<endl;
break;//后续输入跳过
}
}
if(i==m&&rs==1)//如果处理完所有输入都没有形成严格有序的拓扑序列
cout<<"Sorted sequence cannot be determined."<<endl;
}
return 0;
}
[/cpp]
我原本以为又是DFS,又是Floyd,算法时空效率会很低,但是提交后AC,用时125MS,内存244K,也不是很差。
代码中的拓扑排序算法使用的是基于DFS的版本,大家也可以改成Kahn算法。
如果觉得自己的代码是对的,但是提交WA的,可以使用这两个测试数据: Input
The input data will start with the number of the test cases. For each test case, 9 lines follow, corresponding to the rows of the table. On each line a string of exactly 9 decimal digits is given, corresponding to the cells in this line. If a cell is empty it is represented by 0.
Output
For each test case your program should print the solution in the same format as the input data. The empty cells have to be filled according to the rules. If solutions is not unique, then the program may print any one of them.
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
Source
Southeastern Europe 2005
Input
The input data will start with the number of the test cases. For each test case, 9 lines follow, corresponding to the rows of the table. On each line a string of exactly 9 decimal digits is given, corresponding to the cells in this line. If a cell is empty it is represented by 0.
Output
For each test case your program should print the solution in the same format as the input data. The empty cells have to be filled according to the rules. If solutions is not unique, then the program may print any one of them.
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
Source
Southeastern Europe 2005