POJ 1080-Human Gene Functions Human Gene Functions Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 17334 Accepted: 9637 Description It is well known that a human gene can be considered as a sequence, consisting of four nucleotides, which are simply denoted by four letters, A, C, G, and T. Biologists have been interested in identifying human genes and determining their functions, because these can be used to diagnose human diseases and to design new drugs for them. A human gene can be identified through a series of time-consuming biological experiments, often with the help of computer programs. Once a sequence of a gene is obtained, the next job is to determine its function. One of the methods for biologists to use in determining the function of a new gene sequence that they have just identified is to search a database with the new gene as a query. The database to be searched stores many gene sequences and their functions – many researchers have been submitting their genes and functions to the database and the database is freely accessible through the Internet. A database search will return a list of gene sequences from the database that are similar to the query gene. Biologists assume that sequence similarity often implies functional similarity. So, the function of the new gene might be one of the functions that the genes from the list have. To exactly determine which one is the right one another series of biological experiments will be needed. Your job is to make a program that compares two genes and determines their similarity as explained below. Your program may be used as a part of the database search if you can provide an efficient one. Given two genes AGTGATG and GTTAG, how similar are they? One of the methods to measure the similarity of two genes is called alignment. In an alignment, spaces are inserted, if necessary, in appropriate positions of the genes to make them equally long and score the resulting genes according to a scoring matrix. For example, one space is inserted into AGTGATG to result in AGTGAT-G, and three spaces are inserted into GTTAG to result in –GT–TAG. A space is denoted by a minus sign (-). The two genes are now of equal length. These two strings are aligned: AGTGAT-G -GT–TAG In this alignment, there are four matches, namely, G in the second position, T in the third, T in the sixth, and G in the eighth. Each pair of aligned characters is assigned a score according to the following scoring matrix. 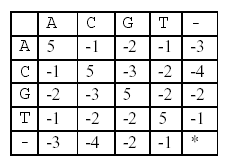 denotes that a space-space match is not allowed. The score of the alignment above is (-3)+5+5+(-2)+(-3)+5+(-3)+5=9. Of course, many other alignments are possible. One is shown below (a different number of spaces are inserted into different positions): AGTGATG -GTTA-G This alignment gives a score of (-3)+5+5+(-2)+5+(-1) +5=14. So, this one is better than the previous one. As a matter of fact, this one is optimal since no other alignment can have a higher score. So, it is said that the similarity of the two genes is 14. Input The input consists of T test cases. The number of test cases ) (T is given in the first line of the input file. Each test case consists of two lines: each line contains an integer, the length of a gene, followed by a gene sequence. The length of each gene sequence is at least one and does not exceed 100. Output The output should print the similarity of each test case, one per line. Sample Input 2 7 AGTGATG 5 GTTAG 7 AGCTATT 9 AGCTTTAAA Sample Output 14 21 Source Taejon 2001
这一题是LCS(最长公共子序列)的变种,但是还是用DP来解决。 题目问给两个基因序列s1,s2插入’-‘,使得两个序列的`相似度`最大,求最大的相似度。假设f[i-1,j-1]为s1[1,…,i-1]和s2[1,…,j-1]的最大相似度,怎么通过f[i-1,j-1]来求f[i,j]呢?分如下三种情况:(这里假设f下标从0开始,s1,s2下标从1开始) 1. s1取第i个基因,s2取’-‘,则f[i,j]=f[i-1,j]+score[s1[i]],’-‘]; 2. s1取’-‘,s2取第j个基因,则f[i,j]=f[i,j-1]+score[‘-‘,s2[j]]; 3. s1取第i个基因,s2取第j个基因,则f[i,j]=f[i-1,j-1]+score[s1[i],s2[j]]; 所以f[i,j]即为上述三者的最大值。 对于初始值,自然有f[0,0]=0; f[0,j]=f[0,j-1]+score[‘-‘,s2[j]]; f[i,0]=f[i-1,0]+score[s1[i],’-‘]。 有了上述状态转换方程及初始值,便可以写出DP代码: [cpp] #include<iostream> #include<string> using namespace std; int score[‘T’+1][‘T’+1]; int inf=-5;//负无穷 const int MAX_N=101;//基因最大长度 int f[MAX_N][MAX_N];//f[i][j]表示s1[0…i-1]和s2[0…j-1]的相识度 //初始化分数表 void init_score() { score[‘A’][‘A’]=score[‘C’][‘C’]=score[‘G’][‘G’]=score[‘T’][‘T’]=5;//可以连续赋值 score[‘-‘][‘-‘]=inf;//负无穷 score[‘A’][‘C’]=score[‘C’][‘A’]=-1; score[‘A’][‘G’]=score[‘G’][‘A’]=-2; score[‘A’][‘T’]=score[‘T’][‘A’]=-1; score[‘A’][‘-‘]=score[‘-‘][‘A’]=-3;//’-‘的ASCII小于’T’ score[‘C’][‘G’]=score[‘G’][‘C’]=-3; score[‘C’][‘T’]=score[‘T’][‘C’]=-2; score[‘C’][‘-‘]=score[‘-‘][‘C’]=-4; score[‘G’][‘T’]=score[‘T’][‘G’]=-2; score[‘G’][‘-‘]=score[‘-‘][‘G’]=-2; score[‘T’][‘-‘]=score[‘-‘][‘T’]=-1; } //动态规划求值 int DP(string s1,int n1,string s2,int n2) { f[0][0]=0; for(int i=1;i<=n1;i++) //f[0][i]=f[0][i-1]+score[‘-‘][s1[i-1]];//注意顺序不要弄错了,这里表示i,s1为纵轴;j,s2为横轴 f[i][0]=f[i-1][0]+score[s1[i-1]][‘-‘]; for(int j=1;j<=n2;j++) //f[j][0]=f[j-1][0]+score[s2[j-1]][‘-‘]; f[0][j]=f[0][j-1]+score[‘-‘][s2[j-1]]; for(int i=1;i<=n1;i++) { for(int j=1;j<=n2;j++) { int a=f[i-1][j]+score[s1[i-1]][‘-‘]; int b=f[i][j-1]+score[‘-‘][s2[j-1]]; int c=f[i-1][j-1]+score[s1[i-1]][s2[j-1]]; int rs=a>b?a:b; f[i][j]=rs>c?rs:c;//三者最大值 } } return f[n1][n2]; } int main() { //freopen("input.txt","r",stdin); int t; cin>>t; init_score(); while(t–) { int n1,n2; string s1,s2; cin>>n1>>s1>>n2>>s2; cout<<DP(s1,n1,s2,n2)<<endl; } return 0; } [/cpp] 本代码提交AC,用时0MS,内存272K。]]>